题目内容
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,解不等式
时,解不等式![]() ;
;
(Ⅱ)若![]() 的图象与x轴围成图形的面积大于6,求实数a的取值范围.
的图象与x轴围成图形的面积大于6,求实数a的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
(Ⅰ)去绝对值,然后得到![]() ,或
,或![]() ,或
,或![]() ,解不等式组即可;
,解不等式组即可;
(Ⅱ)![]() 时,
时,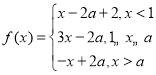 ,然后分
,然后分![]() 和
和![]() ,两种情况求出围成图形的面积即可.
,两种情况求出围成图形的面积即可.
解:(Ⅰ)当![]() 时,
时,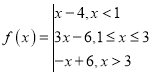
所以原不等式等价于:①![]() 或②
或②![]() 或③
或③![]() .
.
解①得:![]() ;解②得
;解②得![]() ;解③得
;解③得![]() .
.
综上可知,不等式![]() 的解集为
的解集为![]() .
.
(Ⅱ)因为![]() ,故
,故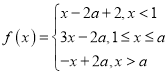
由函数的单调性可知,当![]() 时,
时,![]() ,设
,设![]() ,
,
当![]() 时,由
时,由![]() ,得
,得![]() ,
,![]() 的图像与x轴一个交点为
的图像与x轴一个交点为![]() .
.
当![]() 时,又
时,又![]() ,设点
,设点![]() ,
,
①若![]() ,
,
由![]() 得
得![]() ,设点
,设点![]() ,
,
此时![]() 的图象与x轴另一个交点为
的图象与x轴另一个交点为![]() ,
,
![]() 的图象与x轴周成图形为凹四边形AMNB,其面积为
的图象与x轴周成图形为凹四边形AMNB,其面积为
![]() ,
,
因为![]() ,所以
,所以![]() ,不满足条件.
,不满足条件.
②若![]() ,由
,由![]() ,得
,得![]() ,设点
,设点![]() ,
,
![]() 的图象与x轴围成图形为三角形AMC,其面积为
的图象与x轴围成图形为三角形AMC,其面积为
![]() ,
,
由已知得![]() ,又
,又![]() ,所以
,所以![]() ,
,
综上,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
【题目】某中学为了解中学生的课外阅读时间,决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20名学生,对他们的课外阅读时间进行问卷调查.现在按课外阅读时间的情况将学生分成三类:![]() 类(不参加课外阅读),
类(不参加课外阅读),![]() 类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),
类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),![]() 类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时).调查结果如下表:
类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时).调查结果如下表:
|
|
| |
男生 |
| 5 | 3 |
女生 |
| 3 | 3 |
(1)求出表中![]() ,
,![]() 的值;
的值;
(2)根据表中的统计数据,完成下面的列联表,并判断是否有90%的把握认为“参加课外阅读与否”与性别有关;
男生 | 女生 | 总计 | ||
不参加课外阅读 | ||||
参加课外阅读 | ||||
总计 |
P(K≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

