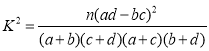题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ; (2)见解析
; (2)见解析
【解析】
(1)代入![]() ,可得
,可得![]() 的解析式.求得导函数,即可得直线方程的斜率,求得点坐标后,由点斜式即可求得切线方程.
的解析式.求得导函数,即可得直线方程的斜率,求得点坐标后,由点斜式即可求得切线方程.
(2)根据放缩法,由![]() 得
得![]() .从而证明
.从而证明![]() 即可.构造函数
即可.构造函数![]() ,通过求得导函数
,通过求得导函数![]() ,再令
,再令![]() ,求得
,求得![]() .即可判断
.即可判断![]() 的单调性,进而求得
的单调性,进而求得![]() 的零点所在区间,并判断出该零点为
的零点所在区间,并判断出该零点为![]() 的极小值点,求得在该点的最小值,即证明不等式成立.
的极小值点,求得在该点的最小值,即证明不等式成立.
(1)当![]() 时,
时,![]()
所以![]()
所以![]() ,又因为
,又因为![]() ,即点坐标为
,即点坐标为![]()
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
即![]()
(2)证明:当![]() 时,
时,![]() ,
,
要证明![]() ,需证明
,需证明![]() ,
,
设![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,
,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,
,![]() ,
,
所以函数![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,且
,且![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,
,
故![]() ,
,![]()
综上可知,若![]() ,
,![]() .
.

 全能练考卷系列答案
全能练考卷系列答案【题目】为了研究55岁左右的中国人睡眠质量与心脑血管病是否有关联,某机构在适龄人群中随机抽取了100万个样本,调查了他们每周是否至少三个晚上出现了三种失眠症状,![]() 症状:入睡困难;
症状:入睡困难;![]() 症状:醒得太早;
症状:醒得太早;![]() 症状:不能深度入睡或做梦,得到的调查数据如下:
症状:不能深度入睡或做梦,得到的调查数据如下:
数据1:出现![]() 症状人数为8.5万,出现
症状人数为8.5万,出现![]() 症状人数为9.3万,出现
症状人数为9.3万,出现![]() 症状人数为6.5万,其中含
症状人数为6.5万,其中含![]() 症状同时出现1.8万人,
症状同时出现1.8万人,![]() 症状同时出现1万人,
症状同时出现1万人,![]() 症状同时出现2万人,
症状同时出现2万人,![]() 症状同时出现0.5万人;
症状同时出现0.5万人;
数据2:同时有失眠症状和患心脑血管病的人数为5万人,没有失眠症状且无心脑血管病的人数为73万人.
(Ⅰ)依据上述数据试分析55岁左右的中国人患有失眠症的比例大约多少?
(Ⅱ)根据以上数据完成如下列联表,并根据所填列联表判断能否有95%的把握说明失眠与心脑血管病存在“强关联”?
失眠 | 不失眠 | 合计 | |
患心脑血管疾病 | |||
不患心脑血管疾病 | |||
合计 |
参考数据如下:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: