题目内容
【题目】已知抛物线![]() 的顶点为
的顶点为![]() ,焦点
,焦点![]() .
.

(1)求抛物线![]() 的方程;
的方程;
(2)过![]() 作直线交抛物线于
作直线交抛物线于![]() 、
、![]() 两点.若直线
两点.若直线![]() 、
、![]() 分别交直线
分别交直线![]() :
:![]() 于
于![]() 、
、![]() 两点,求
两点,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由抛物线的几何性质及题设条件焦点![]() ,可直接求得
,可直接求得![]() ,确定出抛物线的开口方向,写出物线
,确定出抛物线的开口方向,写出物线![]() 的标准方程.
的标准方程.
(2)由题意,可![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,将直线方程与抛物线方程联立,写出韦达定理,再结合弦长公式求出
,将直线方程与抛物线方程联立,写出韦达定理,再结合弦长公式求出![]() ,分别求出
,分别求出![]() 和
和![]() 即可表示出
即可表示出![]() ,最后利用换元法和二次函数,即可求得
,最后利用换元法和二次函数,即可求得![]() 最小值.
最小值.
()由题意可设抛物线![]() 的方程为
的方程为![]() ,则
,则![]() ,解得
,解得![]() ,
,
故抛物线![]() 的方程为
的方程为![]() ;
;
(2)设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
由![]() 消去
消去![]() ,整理得
,整理得![]() ,
,
所以![]() ,
,![]() ,
,
从而有![]() ,
,
由 解得点
解得点![]() 的横坐标为
的横坐标为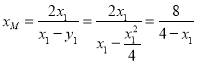 ,
,
同理可得点![]() 的横坐标为
的横坐标为![]() ,
,
所以
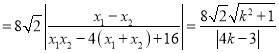 ,
,
令![]() ,
,![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,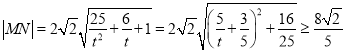 ,
,
综上所述,当![]() ,即
,即![]() 时,
时,![]() 的最小值是
的最小值是![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】武汉有“九省通衢”之称,也称为“江城”,是国家历史文化名城.其中著名的景点有黄鹤楼、户部巷、东湖风景区等等.
(1)为了解“五·一”劳动节当日江城某旅游景点游客年龄的分布情况,从年龄在22岁到52岁的游客中随机抽取了1000人,制成了如图的频率分布直方图:
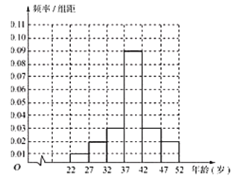
现从年龄在![]() 内的游客中,采用分层抽样的方法抽取10人,再从抽取的10人中随机抽取4人,记4人中年龄在
内的游客中,采用分层抽样的方法抽取10人,再从抽取的10人中随机抽取4人,记4人中年龄在![]() 内的人数为
内的人数为![]() ,求
,求![]() ;
;
(2)为了给游客提供更舒适的旅游体验,该旅游景点游船中心计划在2020年劳动节当日投入至少1艘至多3艘![]() 型游船供游客乘坐观光.由2010到2019这10年间的数据资料显示每年劳动节当日客流量
型游船供游客乘坐观光.由2010到2019这10年间的数据资料显示每年劳动节当日客流量![]() (单位:万人)都大于1.将每年劳动节当日客流量数据分成3个区间整理得表:
(单位:万人)都大于1.将每年劳动节当日客流量数据分成3个区间整理得表:
劳动节当日客流量 |
|
|
|
频数(年) | 2 | 4 | 4 |
以这10年的数据资料记录的3个区间客流量的频率作为每年客流量在该区间段发生的概率,且每年劳动节当日客流量相互独立.
该游船中心希望投入的![]() 型游船尽可能被充分利用,但每年劳动节当日
型游船尽可能被充分利用,但每年劳动节当日![]() 型游船最多使用量(单位:艘)要受当日客流量
型游船最多使用量(单位:艘)要受当日客流量![]() (单位:万人)的影响,其关联关系如下表:
(单位:万人)的影响,其关联关系如下表:
劳动节当日客流量 |
|
| |
| 1 | 2 | 3 |
若某艘![]() 型游船在劳动节当日被投入且被使用,则游船中心当日可获得利润3万元;若某艘
型游船在劳动节当日被投入且被使用,则游船中心当日可获得利润3万元;若某艘![]() 型游船劳动节当日被投入却不被使用,则游船中心当日亏损0.5万元.记
型游船劳动节当日被投入却不被使用,则游船中心当日亏损0.5万元.记![]() (单位:万元)表示该游船中心在劳动节当日获得的总利润,
(单位:万元)表示该游船中心在劳动节当日获得的总利润,![]() 的数学期望越大游船中心在劳动节当日获得的总利润越大,问该游船中心在2020年劳动节当日应投入多少艘
的数学期望越大游船中心在劳动节当日获得的总利润越大,问该游船中心在2020年劳动节当日应投入多少艘![]() 型游船才能使其当日获得的总利润最大?
型游船才能使其当日获得的总利润最大?