题目内容
17．已知函数f（x）=ax3+bx+4（a，b∈R），f（lg（log210））=5，则f（lg（lg2））=3．分析 构造函数f（x）=g（x）+4，得出函数g（x）=ax3+bx是奇函数，由g（lg（log210））+g（lg（lg2））=0求出f（lg（lg2））的值．
解答 解：∵函数f（x）=ax3+bx+4（a，b∈R），
且lg（log210）+lg（lg2）=lg1=0，
∴lg（log210）与lg（lg2）互为相反数；
令f（x）=g（x）+4，
即g（x）=ax3+bx是一个奇函数，
故g（lg（log210））+g（lg（lg2））=0；
∴f（lg（log210））+f（lg（lg2））
=g（lg（log210））+4+g（lg（lg2））+4=8；
又f（lg（log210））=5，
∴f（lg（lg2））=8-5=3．
故答案为：3．
点评 本题考查了利用函数的奇偶性求函数值的问题，是基础题目．
练习册系列答案
相关题目
2．
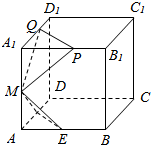如图：已知棱长为l的正方体ABCD-A1B1C1D1中，E，F，M分别是AB、AD、AA1的中点，又P、Q分别在线段A1B1、A1D1上，且A1P=A1Q=x，0＜x＜1，设平面MEF∩平面MPQ=l，则下列结论中不成立的是（ ）
如图：已知棱长为l的正方体ABCD-A1B1C1D1中，E，F，M分别是AB、AD、AA1的中点，又P、Q分别在线段A1B1、A1D1上，且A1P=A1Q=x，0＜x＜1，设平面MEF∩平面MPQ=l，则下列结论中不成立的是（ ）| A． | l∥平面ABCD | B． | 平面MEF与平面MPQ不垂直 | ||
| C． | l⊥BC1 | D． | 当x变化时，l是定直线 |
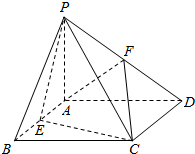如图，四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD是矩形，E、F别是AB、PD的中点．若PA=AD=CD=4．