题目内容
7.过抛物线y2=2px(p>0)的焦点的一条直线与它交于P,Q两点,过点P和此抛物线顶点的直线与准线交于点M.求证直线MQ平行于此抛物线的对称轴.分析 设直线PQ为x-$\frac{p}{2}$=ky,即x=ky+$\frac{p}{2}$,代入抛物线y2=2px,得到y2-2pky-p2=0,由韦达定理得y1•y2=-p2;再证明M,Q的纵坐标相同即可.
解答 证明:抛物线y2=2px的焦点坐标为($\frac{p}{2}$,0),
设直线PQ为x-$\frac{p}{2}$=ky,即x=ky+$\frac{p}{2}$,
代入抛物线y2=2px得:
y2=2p(ky+$\frac{p}{2}$),即y2-2pky-p2=0
由韦达定理得:y1•y2=-p2;
直线OP的方程为y=$\frac{{y}_{1}}{{x}_{1}}$•x,
x=-$\frac{p}{2}$时,y=-$\frac{{y}_{1}}{{x}_{1}}$•$\frac{p}{2}$=-$\frac{p}{2}$•$\frac{{y}_{1}}{\frac{{{y}_{1}}^{2}}{2p}}$=-$\frac{{p}^{2}}{{y}_{1}}$=y2,
即有直线MQ平行于此抛物线的对称轴.
点评 本题考查直线与抛物线之间的关系,利用方程联立得到方程,根据根和系数的关系得到结论是关键.

练习册系列答案
相关题目
16.如图,正方形ABCD中,点E是DC的中点,CF:FB=2:1,那么$\overrightarrow{EF}$=( )
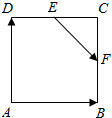

| A. | $\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AD}$ | B. | $\frac{1}{4}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ | C. | $\frac{1}{2}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AD}$ | D. | $\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ |