题目内容
2．命题p：?x∈R，|x+3|+|x-1|+a≤0．若此命题是假命题，则实数a的取值范围是（-4，+∞）（用区间表示）分析 根据特称命题的性质，以及绝对值不等式的解法进行求解．
解答 解：若：?x∈R，|x+3|+|x-1|+a≤0是假命题，
则：?x∈R，|x+3|+|x-1|+a＞0是真命题，
即|x+3|+|x-1|＞-a是真命题，
∵|x+3|+|x-1|≥|-3-1|=4，
∴-a＜4，即a＞-4．
故答案为：（-4，+∞）
点评 本题主要考查特称命题的应用，利用绝对值不等式的解法是解决本题的关键．
练习册系列答案
相关题目
13．已知m、n是不重合的直线，α、β是不重合的平面，则下列命题正确的是（ ）
| A． | 若m?α，n∥α，则m∥n | B． | 若m∥α，m∥β，则α∥β | ||
| C． | 若α∩β=n，m∥n，则m∥β | D． | 若m⊥α，m⊥β，则α∥β |
7．某种产品的广告费支出x与销售额y（单位：百万元）之间有如表对应数据：
（1）求回归直线方程；
（2）试预测广告费支出为10百万元时，销售额多大？
$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{∑（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$．
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
（2）试预测广告费支出为10百万元时，销售额多大？
$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{∑（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$．
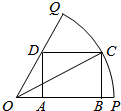如图，已知OPQ是半径为$\sqrt{7}$圆心角为$\frac{π}{3}$的扇形，C是该扇形弧上的动点，ABCD是扇形的内接矩形，记∠BOC为α．