题目内容
5．求函数y=-4sin2x-4cosx+3的最大值和最小值．分析 利用同角三角函数的基本关系化简函数的解析式，再利用二次函数的性质求得函数的最大值和最小值．
解答 解：∵函数y=-4sin2x-4cosx+3=-4（1-cos2x）-4cosx+3=4cos2x-4cosx-1=（2cosx-1）2-2，
故当cosx=-1时，f（x）max=7；当cosx=$\frac{1}{2}$时，f（x）min=-2．
点评 本题主要考查同角三角函数的基本关系，二次函数的性质应用，属于基础题．
练习册系列答案
相关题目
11．若不等式组$\left\{\begin{array}{l}x≥1\\ y≥0\\ 2x+y≤6\\ x+y≤a\end{array}\right.$表示的平面区域是一个三角形，则实数a的取值范围是（ ）
| A． | {a|1≤a≤3或a＞5} | B． | {a|1＜a≤3或a≥5} | C． | {a|1＜a≤5} | D． | {a|3≤a≤5} |
13．已知m、n是不重合的直线，α、β是不重合的平面，则下列命题正确的是（ ）
| A． | 若m?α，n∥α，则m∥n | B． | 若m∥α，m∥β，则α∥β | ||
| C． | 若α∩β=n，m∥n，则m∥β | D． | 若m⊥α，m⊥β，则α∥β |
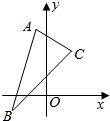已知平行四边形ABCD的三个顶点的坐标为A（-1，4），B（-2，-1），C（2，3）．