题目内容
数列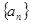 满足:
满足: (
( ),且
),且 ,若数列的前2011项之和为2012,则前2012项的和等于
,若数列的前2011项之和为2012,则前2012项的和等于
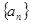 满足:
满足: (
( ),且
),且 ,若数列的前2011项之和为2012,则前2012项的和等于
,若数列的前2011项之和为2012,则前2012项的和等于| A.0 | B.1 | C.2012 | D.2013 |
D
试题分析:假设首项设a1=m,由于a2=1,且an+2=an+1-an∴a3=1-m.a4=-m,a5=-1,a6=m-1,a7=m,a8=1,a9=1-m…,∴数列{an}是周期为6的周期函数,且前6项和为0,∴数列的前2011项之和为m⇒m=2012,2011=6
 335+1,2012=6
335+1,2012=6 335+2,则前2012项的和等于2012+1=2013.故选D.
335+2,则前2012项的和等于2012+1=2013.故选D.点评:解决该试题的关键是可通过递推公式求出数列的前九项,从而确定数列周期为6,再由数列周期从而求解a2011=a1,求出结果.

练习册系列答案
相关题目
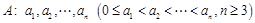 具有性质
具有性质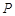 :
: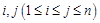 ,
,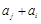 与
与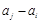 两数中至少有一个是该数列中的一项. 现给出以下四个命题:①数列
两数中至少有一个是该数列中的一项. 现给出以下四个命题:①数列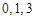 具有性质
具有性质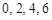 具有性质
具有性质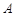 具有性质
具有性质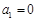 ;
; 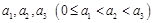 具有性质
具有性质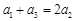 .
. 满足
满足 ,其中
,其中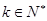 ,设
,设 ,则
,则 等于( ).
等于( ).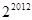
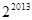


 是公差为
是公差为 的等差数列,且
的等差数列,且 成等比数列,则
成等比数列,则 项和
项和 为( )
为( )




 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( ) 等于( )
等于( )
 则当
则当 时,n的最小值是
时,n的最小值是 对任意的
对任意的 有
有 ,若
,若 ,则
,则 .
.