题目内容
在数列{an}中,a1=2,an+1=an+n,则a100= .
4952
试题分析:由题意知a2-a1=1,a3-a2=2,…,a100-a99=99,所以a100=a1+(a2-a1)+(a3-a2)+…+(a100-a99)=1+1+2+…+99=4951.因此可知a100=a1+(a2-a1)+(a3-a2)+…+(a100-a99)
=2+1+2+…+99=2+
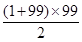 =4952.故答案为4952.
=4952.故答案为4952.点评:解决该试题的关键能根据累加法的思想得到其前n项的和。

练习册系列答案
相关题目
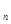 }满足0<a
}满足0<a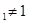 , 且
, 且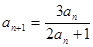 (n
(n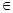 N*).
N*). 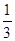 ,求出a2、a3、a4、a5的值,归纳出an , 并用数学归纳法证明.
,求出a2、a3、a4、a5的值,归纳出an , 并用数学归纳法证明.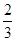 an+
an+ ,则数列{an}的通项公式是an=______.
,则数列{an}的通项公式是an=______. 中,
中, ,
, ,
, ,则
,则
 中
中 ,则
,则 ( )
( )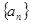 满足:
满足: (
( ),且
),且 ,若数列的前2011项之和为2012,则前2012项的和等于
,若数列的前2011项之和为2012,则前2012项的和等于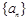 ,通项公式为
,通项公式为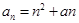 ,若此数列为递增数列,则
,若此数列为递增数列,则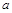 的取值范围是
的取值范围是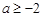
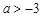
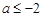
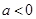
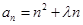 恒成立, 求实数λ的取值范围是
恒成立, 求实数λ的取值范围是 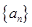 的通项为
的通项为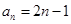 ,
,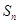 为数列
为数列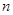 项和,令
项和,令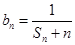 ,则数列
,则数列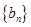 的前
的前


