题目内容
【题目】已知抛物线C:y2=2px(p>0)的焦点F,直线y=4与y轴的交点为P,与抛物线C的交点为Q,且|QF|=2|PQ|.
(1)求p的值;
(2)已知点T(t,-2)为C上一点,M,N是C上异于点T的两点,且满足直线TM和直线TN的斜率之和为![]() ,证明直线MN恒过定点,并求出定点的坐标.
,证明直线MN恒过定点,并求出定点的坐标.
【答案】(1)p=4 (2)证明见解析,定点坐标:(-1,-1)
【解析】
(1)设Q(x0,4),由抛物线定义,根据|QF|=x0+![]() ,解得x0=
,解得x0=![]() ,将点Q
,将点Q![]() 代入抛物线方程,即可求解;
代入抛物线方程,即可求解;
(2)设直线MN的方程为x=my+n,代入抛物线的方程,代入y1+y2,y1y2,结合斜率公式,求得n=m-1,代入直线方程,即可求解.
(1)设Q(x0,4),由抛物线定义,|QF|=x0+![]() ,
,
又|QF|=2|PQ|,即2x0=x0+![]() ,解得x0=
,解得x0=![]() ,
,
将点Q![]() 代入抛物线方程,解得p=4.
代入抛物线方程,解得p=4.
(2)由(1)知C的方程为y2=8x,所以点T坐标为![]() ,
,
设直线MN的方程为x=my+n,点M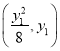 ,N
,N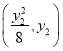 ,
,
由![]() 得y2-8my-8n=0,所以y1+y2=8m,y1y2=-8n,
得y2-8my-8n=0,所以y1+y2=8m,y1y2=-8n,
所以kMT+kNT=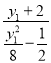 +
+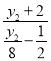 =
=![]() +
+![]()
=![]() =
=![]() =-
=-![]() ,
,
解得n=m-1,所以直线MN方程为x+1=m(y+1),
此时直线恒过点(-1,-1).

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目