题目内容
【题目】已知椭圆C：
的焦距为
，短半轴的长为2，过点P(－2,1)且斜率为1的直线l与椭圆C交于A，B两点．
(1)求椭圆C的方程；
(2)求弦AB的长．
【答案】（1）
；（2）
.
【解析】
（1）已知：2c=4
，b=2，a2=b2+c2，联立解得a,b,c的值，即可得椭圆方程；
（2）易得直线l的方程y=x+3．设A（x1，y1），B（x2，y2）．与椭圆方程联立化为：4x2+18x+15=0，利用根与系数的关系及弦长公式即可得出弦AB的长．
(1)已知椭圆焦距为
，短半轴的长为2，即2c=4，b=2，
结合a2=b2+c2，解得a=
，b=2，c=2
故C：
.
(2)已知直线l过点P(－2,1)且斜率为1，故直线方程为y-1=x+2，整理得y=x+3，
直线方程与椭圆方程联立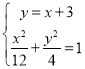
得
. 设
，
．
∴
∴
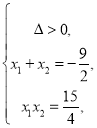
练习册系列答案
相关题目
