题目内容
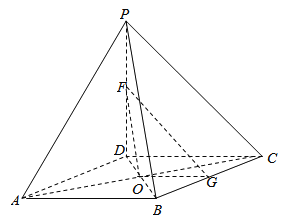
【题目】已知四棱锥![]() 的底面ABCD是菱形,
的底面ABCD是菱形,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,F,G分别为PD,BC中点,
,F,G分别为PD,BC中点,![]() .
.

(Ⅰ)求证:![]() 平面PAB;
平面PAB;
(Ⅱ)求三棱锥![]() 的体积;
的体积;
(Ⅲ)求证:OP与AB不垂直.
【答案】(Ⅰ)见解析(Ⅱ)![]() (Ⅲ)见解析
(Ⅲ)见解析
【解析】
(Ⅰ)连接![]() ,
,![]() ,由已知结合三角形中位线定理可得
,由已知结合三角形中位线定理可得![]() 平面
平面![]() ,再由面面平行的判断可得平面
,再由面面平行的判断可得平面![]() 平面
平面![]() ,进而可得
,进而可得![]() 平面
平面![]() ;
;
(Ⅱ)首先证明![]() 平面
平面![]() ,而
,而![]() 为
为![]() 的中点,然后利用等积法求三棱锥
的中点,然后利用等积法求三棱锥![]() 的体积;
的体积;
(Ⅲ)直接利用反证法证明![]() 与
与![]() 不垂直.
不垂直.
(Ⅰ)如图,连接![]() ,
,![]()
∵![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,
中点,
∴![]() ,而
,而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,
中点,
∴![]() ,而
,而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,又
,又![]()
∴平面![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() .
.
(Ⅱ)∵![]() 底面
底面![]() ,
,
∴![]() ,又四边形
,又四边形![]() 为菱形,
为菱形,
∴![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() ,而
,而![]() 为
为![]() 的中点,
的中点,
∴![]() .
.
(Ⅲ)假设![]() ,又
,又![]() ,且
,且![]() ,
,
∴![]() 平面
平面![]() ,则
,则![]() ,与
,与![]() 矛盾,
矛盾,
∴假设错误,故![]() 与
与![]() 不垂直.
不垂直.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】已知空间四边形ABCD,∠BAC=![]() ,AB=AC=2
,AB=AC=2![]() ,BD=CD=6,且平面ABC⊥平面BCD,则空间四边形ABCD的外接球的表面积为( )
,BD=CD=6,且平面ABC⊥平面BCD,则空间四边形ABCD的外接球的表面积为( )
A. 60π B. 36π C. 24π D. 12π
【题目】某校有1400名考生参加市模拟考试,现采取分层抽样的方法从
文、理考生中分别抽取20份和50份数学试卷,进行成绩分析,
得到下面的成绩频数分布表:
分数分组 | [0,30) | [30,60) | [60,90) | [90,120) | [120,150] |
文科频数 | 2 | 4 | 8 | 3 | 3 |
理科频数 | 3 | 7 | 12 | 20 | 8 |
(1)估计文科数学平均分及理科考生的及格人数(90分为及格分数线);
(2)在试卷分析中,发现概念性失分非常严重,统计结果如下:
文理 失分 | 文 | 理 |
概念 | 15 | 30 |
其它 | 5 | 20 |
问是否有90%的把握认为概念失分与文、理考生的不同有关?(本题可以参考独立性检验临界值表:)
| <>0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:  ,其中
,其中![]() .
.

