[题目]给出下列命题.其中所有正确命题的序号是．①抛物线的准线方程为,②过点作与抛物线只有一个公共点的直线仅有1条,③是抛物线上一动点.以为圆心作与抛物线准线相切的圆.则此圆一定过定点.④抛物线上到直线距离最短的点的坐标为. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】给出下列命题，其中所有正确命题的序号是__________．

①抛物线的准线方程为；

②过点作与抛物线只有一个公共点的直线仅有1条；

③是抛物线上一动点，以为圆心作与抛物线准线相切的圆，则此圆一定过定点.

④抛物线上到直线距离最短的点的坐标为.

【答案】③④

【解析】

运用直线与抛物线的位置关系分别判定命题的正确性

①抛物线的标准方程为不是；故错误

②过点作与抛物线只有一个公共点的直线有两条，一条是过点与抛物线相切的直线，一条是过点平行于轴的直线，故错误

③设,则以P为圆心，作与抛物线准线相切的圆的方程为,化简可得,当时恒成立，故此圆一定过定点，故正确

④设抛物线上到直线距离最短的点的坐标为

则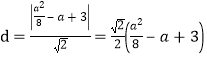

当时，取最小值

则抛物线上到直线距离最短的点的坐标为，故正确

综上其中所有正确命题的序号为③④

练习册系列答案

相关题目

【题目】是抛物线为上的一点，以S为圆心，r为半径做圆，分别交x轴于A，B两点，连结并延长SA、SB，分别交抛物线于C、D两点．

求抛物线的方程．

求证：直线CD的斜率为定值．

【题目】已知点是圆：上任意一点，点与圆心关于原点对称.线段的中垂线与交于点.

（1）求动点的轨迹方程；

（2）设点，若直线轴且与曲线交于另一点，直线与直线交于点，证明：点恒在曲线上，并求面积的最大值.

【题目】下列所给4个图象中，与所给3件事吻合最好的顺序为（）

①我离开学校不久，发现自己把作业本忘在教室，于是立刻返回教室里取了作业本再回家；

②我放学回家骑着车一路以常速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间；

③我放学从学校出发后，心情轻松，缓缓行进，后来为了赶时间开始加速.

A.（1）（2）（4）B.（4）（1）（2）C.（4）（1）（3）D.（4）（2）（3）

【题目】已知f(x)是定义在R上的偶函数，且当x≥0时，f(x)＝loga(x＋1)(a＞0，且a≠1)．

(1)求函数f(x)的解析式；

(2)若－1＜f(1)＜1，求实数a的取值范围．

【题目】李明自主创业，在网上经营一家水果店，销售的水果中有草莓、京白梨、西瓜、桃，价格依次为60元/盒、65元/盒、80元/盒、90元/盒．为增加销量，李明对这四种水果进行促销：一次购买水果的总价达到120元，顾客就少付x元．每笔订单顾客网上支付成功后，李明会得到支付款的80%．

①当x=10时，顾客一次购买草莓和西瓜各1盒，需要支付__________元；

②在促销活动中，为保证李明每笔订单得到的金额均不低于促销前总价的七折，则x的最大值为__________．

【题目】已知函数f（x）=（xR），g（x）=2a-1

（1）求函数f（x）的单调区间与极值．

（2）若f（x）≥g（x）对恒成立，求实数a的取值范围.

【题目】学校选派甲、乙、丙、丁、戊5名学生代表学校参加市级“演讲”和“诗词”比赛，下面是他们的一段对话．甲说：“乙参加‘演讲’比赛”；乙说：“丙参加‘诗词’比赛”；丙说“丁参加‘演讲’比赛”；丁说：“戊参加‘诗词’比赛”；戊说：“丁参加‘诗词’比赛”．

已知这5个人中有2人参加“演讲”比赛，有3人参加“诗词”比赛，其中有2人说的不正确，且参加“演讲”的2人中只有1人说的不正确．根据以上信息，可以确定参加“演讲”比赛的学生是

A. 甲和乙 B. 乙和丙 C. 丁和戊 D. 甲和丁

【题目】某学校900名学生在一次百米测试中，成绩全部介于13秒与18 秒之间，利用分层抽样的方法抽取其中若干个样本，将测试结果按如下方式分成五组：第一组[13,14），第二组[14,15），…，第五组[17,18]，有关数据见下表：

	各组组员数	各组抽取人数
[13,14）	54	a
[14,15）	b	8
[15,16）	342	19
[16,17）	288	c
[17,18]		d

（1）求a,b,c,d的值；

（2）若样本第一组中只有一个女生，其他都是男生，第五组则只有一个男生，其他都是女生，现从第一、五组中各抽一个同学组成一个新的组，求这个新组恰好由一个男生和一个女生构成的概率。

试题分类