题目内容
13.若指数函数f(x)=(a2-1)x在(-∞,+∞)上是减函数,则a的取值范围是( )| A. | |a|>1 | B. | |a||<√2√2 | C. | |a|>√2√2 | D. | 1<|a|<√2√2 |
分析 根据指数函数的单调性构造关于a的不等式,解不等式即可得到结论.
解答 解:∵y=(a2-1)x在定义域内是减函数,
∴0<a2-1<1,即1<a2<2,
解得1<|a|<√2√2,
故选:D
点评 本题主要考查指数函数的图象和性质,比较基础.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
3.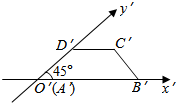 如图是一个水平放置的直观图,它是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积为( )
如图是一个水平放置的直观图,它是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积为( )
 如图是一个水平放置的直观图,它是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积为( )
如图是一个水平放置的直观图,它是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积为( )| A. | 2+√2√2 | B. | 1+√221+√22 | C. | 2+√222+√22 | D. | 1+√2√2 |
4.设C是∠AOB所在平面外的一点,若∠AOB=∠BOC=∠AOC=θ,其中θ是锐角,而OC与平面AOB所成角的余弦值等于√33√33,则θ的值为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
2.已知曲线y=1ex+11ex+1,则曲线的切线斜率取得最小值时的直线方程为( )
| A. | x+4y-2=0 | B. | x-4y+2=0 | C. | 4x+2y-1=0 | D. | 4x-2y-1=0 |
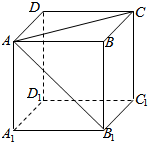 在如图所示的正方体ABCD-A1B1C1D1中,求:
在如图所示的正方体ABCD-A1B1C1D1中,求: