题目内容
定义在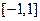 上的函数
上的函数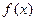 满足
满足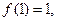 且当
且当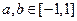 时,
时,
都有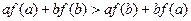 ;
;
(1)判断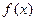 在
在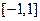 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.
(2)若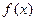 是奇函数, 不等式
是奇函数, 不等式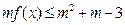 对所有的
对所有的 恒成立,
恒成立,
求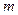 的取值范围.
的取值范围.
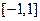 上的函数
上的函数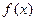 满足
满足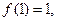 且当
且当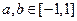 时,
时,都有
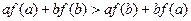 ;
;(1)判断
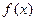 在
在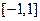 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.(2)若
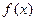 是奇函数, 不等式
是奇函数, 不等式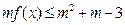 对所有的
对所有的 恒成立,
恒成立,求
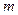 的取值范围.
的取值范围.(1)见解析 (2)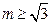 或
或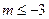 .
.
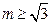 或
或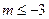 .
.(1)证明:设 令
令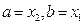 ,
,
则
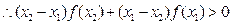 ,
,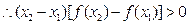
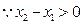 ,
,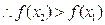 ,
,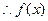 在[-1,1]上是增函数.
在[-1,1]上是增函数.
(2)当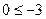 时,
时, 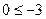 不成立(舍去)
不成立(舍去)
当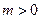 时,
时, 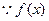 在[-1,1]上是增函数,
在[-1,1]上是增函数, 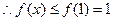
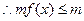
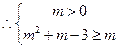

当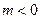 时,
时, 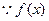 是奇函数,
是奇函数, 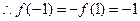 ,
,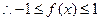 ,
,
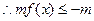
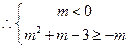
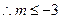
综上所述: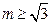 或
或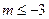 .
.
 令
令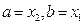 ,
,则

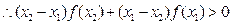 ,
,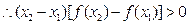
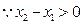 ,
,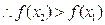 ,
,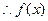 在[-1,1]上是增函数.
在[-1,1]上是增函数. (2)当
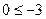 时,
时, 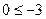 不成立(舍去)
不成立(舍去)当
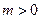 时,
时, 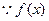 在[-1,1]上是增函数,
在[-1,1]上是增函数, 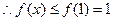
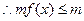
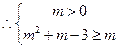

当
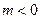 时,
时, 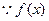 是奇函数,
是奇函数, 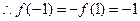 ,
,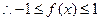 ,
,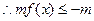
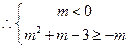
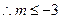
综上所述:
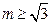 或
或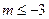 .
.
练习册系列答案
相关题目
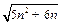 ,汛期共计约40天,当前水库水位为220(标高),而水库警戒水位是400(标高),水库共有水闸15个,每开启一个泄洪,一天可使水位下降4(标高).
,汛期共计约40天,当前水库水位为220(标高),而水库警戒水位是400(标高),水库共有水闸15个,每开启一个泄洪,一天可使水位下降4(标高).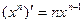 ,
,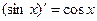 ,
,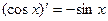 ,是否可判断,可导的奇函数的导函数是偶函数,可导的偶函数的导函数是奇函数。
,是否可判断,可导的奇函数的导函数是偶函数,可导的偶函数的导函数是奇函数。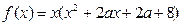 有三个零点
有三个零点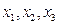 ,且
,且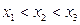 .
. 的取值范围;
的取值范围;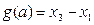 ,求函数
,求函数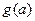 的值域.
的值域.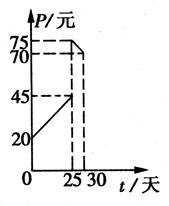
 10
10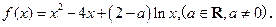
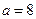 时,求函数
时,求函数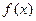 的单调区间;
的单调区间;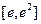 上的最小值.
上的最小值.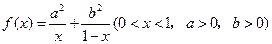 的最值。
的最值。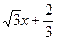 上的任意一点,P点处切线倾斜角为α,则角α的取值范围是 。
上的任意一点,P点处切线倾斜角为α,则角α的取值范围是 。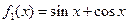 ,记
,记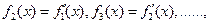
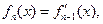
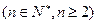 ,则
,则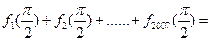 ________.
________.