题目内容
已知数列{an}满足a1=3,an+1=an+p·3n(n∈N*,p为常数),a1,a2+6,a3成等差数列.
(1)求p的值及数列{an}的通项公式;
(2)设数列{bn}满足bn=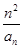 ,证明:bn≤
,证明:bn≤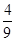 .
.
(1)求p的值及数列{an}的通项公式;
(2)设数列{bn}满足bn=
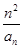 ,证明:bn≤
,证明:bn≤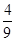 .
.(1)an=3n(2)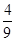
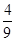
由a1=3,an+1=an+p·3n,得a2=3+3p,a3=a2+9p=3+12p.
∵a1,a2+6,a3成等差数列,∴a1+a3=2(a2+6),即3+3+12p=2(3+3p+6),得p=2.
依题意知,an+1=an+2×3n,
当n≥2时,a2-a1=2×31,a3-a2=2×32,…,an-an-1=2×3n-1.
等号两边分别相加得an-a1=2(31+32+…+3n-1)=2×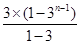 =3n-3,
=3n-3,
∴an-a1=3n-3,∴an=3n(n≥2).
又a1=3适合上式,故an=3n.
(2)证明:∵an=3n,∴bn= .
.
∵bn+1-bn=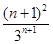 -
- =
= (n∈N*).
(n∈N*).
若-2n2+2n+1<0,则n>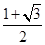 ,
,
即当n≥2时,有bn+1<bn.
又因为b1= ,b2<
,b2<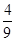 .故bn≤
.故bn≤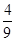
∵a1,a2+6,a3成等差数列,∴a1+a3=2(a2+6),即3+3+12p=2(3+3p+6),得p=2.
依题意知,an+1=an+2×3n,
当n≥2时,a2-a1=2×31,a3-a2=2×32,…,an-an-1=2×3n-1.
等号两边分别相加得an-a1=2(31+32+…+3n-1)=2×
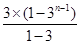 =3n-3,
=3n-3,∴an-a1=3n-3,∴an=3n(n≥2).
又a1=3适合上式,故an=3n.
(2)证明:∵an=3n,∴bn=
 .
.∵bn+1-bn=
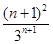 -
- =
= (n∈N*).
(n∈N*).若-2n2+2n+1<0,则n>
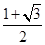 ,
,即当n≥2时,有bn+1<bn.
又因为b1=
 ,b2<
,b2<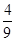 .故bn≤
.故bn≤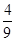

练习册系列答案
相关题目
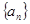 和等比数列
和等比数列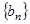 中,
中,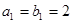 ,
,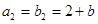 ,
,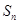 是
是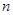 项和.
项和.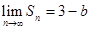 ,求实数
,求实数 的值;
的值;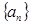 中?若存在,求出所有的
中?若存在,求出所有的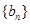 中至少有三项在数列
中至少有三项在数列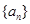 中,但
中,但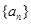 ,公差
,公差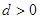 ,前n项和为
,前n项和为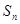 ,
,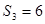 ,且满足
,且满足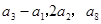 成等比数列.
成等比数列.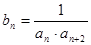 ,求数列
,求数列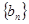 的前
的前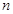 项和
项和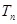 的值.
的值.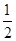 +
+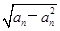 ,且a1=
,且a1=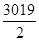
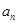 }为等差数列,若
}为等差数列,若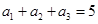 ,
,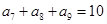 ,则
,则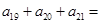 ________.
________.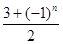 ,数列{an}满足an=d1+d2+d3+…+d2n,又知在数列{bn}中,b1=2,且对任意正整数m,n,
,数列{an}满足an=d1+d2+d3+…+d2n,又知在数列{bn}中,b1=2,且对任意正整数m,n,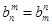 .
.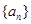 ,如果
,如果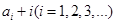 为完全平方数,则称数列
为完全平方数,则称数列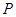 性质”,不论数列
性质”,不论数列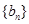 ,且
,且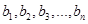 是
是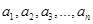 的一个排列;(2)数列
的一个排列;(2)数列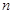 项和;
项和;