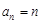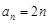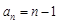题目内容
已知{an}是等差数列,a1=1,公差d≠0,Sn为其前n项和,若a1,a2,a5成等比数列,则S8=________.
64
因为a1,a2,a5成等比数列,则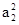 =a1·a5,即(1+d)2=1×(1+4d),解得d=2.所以an=1+(n-1)×2=2n-1,a8=2×8-1=15,S8=
=a1·a5,即(1+d)2=1×(1+4d),解得d=2.所以an=1+(n-1)×2=2n-1,a8=2×8-1=15,S8=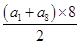 =4×(1+15)=64.
=4×(1+15)=64.
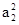 =a1·a5,即(1+d)2=1×(1+4d),解得d=2.所以an=1+(n-1)×2=2n-1,a8=2×8-1=15,S8=
=a1·a5,即(1+d)2=1×(1+4d),解得d=2.所以an=1+(n-1)×2=2n-1,a8=2×8-1=15,S8=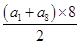 =4×(1+15)=64.
=4×(1+15)=64.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
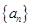 满足:
满足: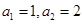 ,且
,且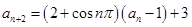 ,
,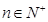 .
.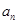 ;
;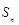
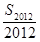 的值为________.
的值为________. a3,2a2成等差数列,则
a3,2a2成等差数列,则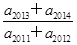 等于( ).
等于( ).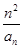 ,证明:bn≤
,证明:bn≤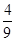 .
. 中,若
中,若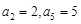 ,则数列
,则数列 的通项公式为( )
的通项公式为( )