题目内容
5.在区间$[{-\frac{π}{2},\frac{π}{2}}]$上随机取一个数x,sinx的值介于$\frac{1}{2}$到1之间的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{π}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 由题意,本题是几何概型的考查,只要求出区间的长度以及满足条件的区间长度,利用公式解答.
解答 解:由题意,区间$[{-\frac{π}{2},\frac{π}{2}}]$的长度为π,在此条件下,满足sinx的值介于$\frac{1}{2}$到1之间的区间是[$\frac{π}{6}$,$\frac{π}{2}$],区间长度为:$\frac{π}{3}$,
由几何概型公式得到sinx的值介于$\frac{1}{2}$到1之间的概率是:$\frac{\frac{π}{3}}{π}=\frac{1}{3}$;
故选:A.
点评 本题考查了几何概型的运用;关键是明确概率模型以及事件的测度,利用公式解答.

练习册系列答案
相关题目
16.已知(a+1)x-1-lnx≤0对于任意$x∈[{\frac{1}{2},2}]$恒成立,则a的最大值为( )
| A. | 0 | B. | 1 | C. | 1-2ln2 | D. | $\frac{-1+ln2}{2}$ |
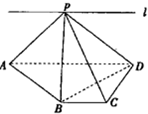 如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD=2,P为平面ABCD外一点,且PB⊥BD.
如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD=2,P为平面ABCD外一点,且PB⊥BD. 已知一个程序语句如图:
已知一个程序语句如图: