题目内容
15.已知函数$f(x)={log_{\frac{1}{2}}}({{x^2}-ax+1})$,若函数的定义域为R,则实数a∈(-2,2);若f(x)的值域为R,则实数a∈(-∞,-2]∪[2,+∞).分析 通过函数$f(x)={log_{\frac{1}{2}}}({{x^2}-ax+1})$的定义域为R可得△=a2-4<0,通过函数$f(x)={log_{\frac{1}{2}}}({{x^2}-ax+1})$的值域为R可得△=a2-4≥0,进而可得结论.
解答 解:若函数$f(x)={log_{\frac{1}{2}}}({{x^2}-ax+1})$的定义域为R,
则有:x2-ax+1>0的解集为R,
∴△=a2-4<0,
∴-2<a<2;
若函数$f(x)={log_{\frac{1}{2}}}({{x^2}-ax+1})$的值域为R,
则有:x2-ax+1>0恒成立,
∴△=a2-4≥0,
∴a≤-2或a≥2;
故答案分别为:(-2,2),(-∞,-2]∪[2,+∞).
点评 本题考查对数函数的简单性质,注意解题方法的积累,属于基础题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
5.在区间$[{-\frac{π}{2},\frac{π}{2}}]$上随机取一个数x,sinx的值介于$\frac{1}{2}$到1之间的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{π}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
10.已知圆O1:(x-1)2+(y+3)2=4,圆O2:(x-2)2+(y+1)2=1,则两圆的位置关系是( )
| A. | 相交 | B. | 内切 | C. | 内含 | D. | 外切 |
20.已知随机变量X服从二项分布X~B(6,$\frac{1}{3}$),则P(X=2)等于( )
| A. | $\frac{13}{16}$ | B. | $\frac{4}{243}$ | C. | $\frac{13}{243}$ | D. | $\frac{80}{243}$ |
4.要得到函数y=2sin(2x+$\frac{π}{3}$)的图象,只需将函数y=2sinx的图象上所有点( )
| A. | 向左平移$\frac{π}{3}$个单位长度,再把横坐标缩短为原来的2倍(纵坐标不变) | |
| B. | 向左平移$\frac{π}{6}$个单位长度,再把横坐标缩短为原来的$\frac{1}{2}$倍(纵坐标不变) | |
| C. | 向左平移$\frac{π}{6}$个单位长度,再把横坐标缩短为原来的2倍(纵坐标不变) | |
| D. | 向左平移$\frac{π}{3}$个单位长度,再把横坐标缩短为原来的$\frac{1}{2}$倍(纵坐标不变) |
5.过曲线y=3x-x3上一点A(2,-2)的切线方程为( )
| A. | y=-2 | B. | 9x+y+16=0 | C. | 9x+y-16=0 | D. | 9x+y-16=0或y=-2 |
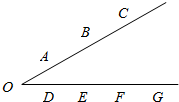 如图,A,B,C三点与D,E,F,G四点分别在一个以O为顶点的角的不同的两边上,则在A,B,C,D,E,F,G,O这8个点中任选三个点作为三角形的三个顶点,可构成的三角形的个数为42.
如图,A,B,C三点与D,E,F,G四点分别在一个以O为顶点的角的不同的两边上,则在A,B,C,D,E,F,G,O这8个点中任选三个点作为三角形的三个顶点,可构成的三角形的个数为42.