题目内容
4.设x=1是函数f(x)=(x2+ax+b)e1-x(x∈R)的一个极值点.(1)求b的值.并用a表示函数f(x)的单凋区间;
(2)设a>0,求函数f(x)在区间[0,4]上的值域.
分析 (1)求出导数,由题意可得f′(1)=0,解得b=1,再对a讨论,a=0,a>0,a<0,解不等式即可得到所求单调区间;
(2)由(1)的a>0的单调区间,讨论a=1,a>1,0<a<1,函数的单调性,求得最值,即可得到所求值域.
解答 解:(1)函数f(x)=(x2+ax+b)e1-x的导数为
f′(x)=(2x+a)•e1-x-(x2+ax+b)•e1-x,
由题意可得f′(1)=0,
即2+a-(1+a+b)=0,
解得b=1;
则f′(x)=-e1-x•(x-1)(x-1+a),
当a=0时,f′(x)≤0,f(x)在R上递减;
当a>0时,1-a<1,f(x)在(1-a,1)上递增,
在(1,+∞),(-∞,1-a)上递减;
当a<0时,1-a>1,f(x)在(1,1-a)上递增,
在(1-a,+∞),(-∞,1)上递减.
(2)由a>0,f(x)=(x2+ax+1)e1-x在(1-a,1)上递增,
在(1,+∞),(-∞,1-a)上递减,
当a=1时,f(x)在(0,1)递增,在(1,4)递减,
则f(x)的最大值为f(1)=3,最小值为f(4)=$\frac{21}{{e}^{3}}$,
即有值域为[$\frac{21}{{e}^{3}}$,3];
当a>1时,1-a<0,则f(x)在(0,1)递增,在(1,4)递减,
则f(x)的最大值为f(1)=2+a,最小值为f(0),f(4)中较小的记为s,
即有值域为[s,2+a];
当0<a<1时,1-a>0,则f(x)在(0,1-a),(1,4)递减,在(1-a,1)递增,
即有f(0)=e,f(1)=2+a,f(1-a)=(2-a)•ea,
f(4)=(17+4a)•e-3,
当a=e-2时,f(x)的最大值为e,最小值为(4e+9)•e-3,
值域为[(4e+9)•e-3,e];
当e-2<a<1时,f(x)的最大值为2+a,最小值为f(1-a)和f(4)中的较小的记为m,
值域为[m,2+a];
当0<a<e-2时,f(x)的最大值为e,最小值为f(1-a)和f(4)中的较小的记为n,
值域为[n,e].
点评 本题考查导数的运用:求单调区间和极值,最值,考查函数的值域的求法,运用分类讨论的思想方法是解题的关键.

 阅读快车系列答案
阅读快车系列答案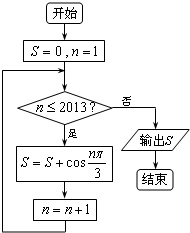
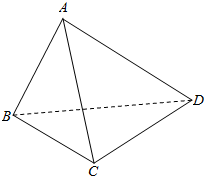 如图,已知三棱锥A-BCD中,△ABC与△ACD均为边长为2的正三角形,BD=$\sqrt{6}$,证明:面ABC⊥面ACD.
如图,已知三棱锥A-BCD中,△ABC与△ACD均为边长为2的正三角形,BD=$\sqrt{6}$,证明:面ABC⊥面ACD.