题目内容
3.已知函数g(x)=alnx+x2-(a+2)x.(1)当a=1时,求函数g(x)的极值;
(2)设定义在D上的函数y=f(x)在点P(m,f(m))处的切线方程为l:y=h(x),当x≠m,若$\frac{f(x)-h(x)}{x-m}$>0在D内恒成立,则称P为函数y=f(x)的“界点”.当a=8时,问函数y=g(x)是否存在“界点”?若存在,求出“界点”的坐标;若不存在,请说明理由.
分析 (1)先求导,再判断函数的单调性,即可得到函数的极值;
(2)根据导数的几何意义求出切线方程,再构造函数f(x)=g(x)-h(x),利用导数和界点的定义,分类讨论即可求出.
解答 解:(1)当a=1时,g(x)=lnx+x2-3x,x>0,
∴g′(x)=$\frac{1}{x}$+2x-3=$\frac{2{x}^{2}-3x+1}{x}$=$\frac{(2x-1)(x-1)}{x}$,
令g′(x)=0,解得x=$\frac{1}{2}$或x=1,
当g′(x)>0时,即0<x<$\frac{1}{2}$,或x>1时,函数g(x)单调递增,
当g′(x)<0时,即$\frac{1}{2}$<x<1时,函数g(x)单调递减,
∴当x=$\frac{1}{2}$时,函数g(x)有极大值,即g($\frac{1}{2}$)=-$\frac{5}{4}$-ln2,
当x=1时,函数g(x)有极小值,即g(1)=-2;
(Ⅱ)a=8时,g(x)=8lnx+x2-10x,
∴g′(x)=$\frac{8}{x}$+2x-10,
由y=g(x)在其图象上一点P(m,f(m))处的切线方程,
得h(x)=(2m+$\frac{8}{m}$-10)(x-m)-8lnm-m2+10m,
∴h′(x)=2m+$\frac{8}{m}$-10,
设f(x)=g(x)-h(x),则f(m)=0,
f′(x)=g′(x)-h′(x)=$\frac{8}{x}$+2x-10-2m-$\frac{8}{m}$+10=$\frac{2}{x}$(x-m)(x-$\frac{4}{m}$),
当0<m<2时,f(x)在(m,$\frac{4}{m}$)上递减,
∴x∈(m,$\frac{4}{m}$)时,f(x)<f(m)=0,此时$\frac{f(x)}{x-m}$<0,
m>2时,f(x)在($\frac{4}{m}$,m)上递减;
∴x∈($\frac{4}{m}$,m)时,f(x)>f(m)=0,此时$\frac{f(x)}{x-m}$<0,
∴y=f(x)在(0,2),(2,+∞)不存在“界点”,
m=2时,f′(x)=$\frac{2}{x}$(x-2)2,即f(x)在(0,+∞)上是增函数;
x>m时,f(x)>f(m)=0,x<m时,f(x)<f(m)=0,
即点P(m,f(m))为“界点”,
故函数y=g(x)存在“界点”,且2是“界点”的横坐标,
∴g(2)=8ln2+4-20=-16+8ln2,
∴“界点”的坐标位(2,-16+8ln2)
点评 本题考查导数和函数的极值的关系,考查类界点的求法.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化,注意导数性质的灵活运用.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
| A. | $\frac{26}{3}$ | B. | $\frac{25}{3}$ | C. | $\frac{22}{3}$ | D. | $\frac{20}{3}$ |

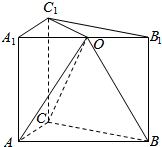 如图,在三棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为A1B1的中点O,且AC:BC:AB:AA1=1:1:$\sqrt{2}$:2.
如图,在三棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为A1B1的中点O,且AC:BC:AB:AA1=1:1:$\sqrt{2}$:2.