题目内容
16.斜率为2的直线l被双曲线$\frac{{x}^{2}}{5}-\frac{{y}^{2}}{4}$=1截得的弦长为2$\sqrt{5}$,则直线l的方程是y=2x±$\frac{12\sqrt{5}}{5}$.分析 先设出直线l的方程,联立双曲线方程,运用韦达定理和判别式大于0,再由弦长公式求出弦长,让弦长为2$\sqrt{5}$,即可求出参数的值.
解答 解:设直线l的方程为y=2x+m,与双曲线交于A,B两点.
设A,B两点的坐标分别为A(x1,y1),B(x2,y2),
将y=2x+m代入双曲线$\frac{{x}^{2}}{5}-\frac{{y}^{2}}{4}$=1,
并整理得:16x2+20mx+5(m2+4)=0,
判别式为400m2-4×16×5(m2+4)>0,
即为m2>16,解得m>4或m<-4.
∴x1+x2=-$\frac{5}{4}$m,x1x2=$\frac{5}{16}$(m2+4),
∴(x1-x2)2=(x1+x2)2-4x1x2=$\frac{25}{16}$m2-$\frac{5}{4}$(m2+4)
∴|AB|2=(1+k2)(x1-x2)2=5(x1-x2)2=$\frac{125}{16}$m2-$\frac{25}{4}$(m2+4)=20,
解得:m=±$\frac{12\sqrt{5}}{5}$.成立.
∴所求直线的方程为:y=2x±$\frac{12\sqrt{5}}{5}$.
故答案为:y=2x±$\frac{12\sqrt{5}}{5}$.
点评 本题考查直线和双曲线的位置关系,主要考查韦达定理和弦长公式的应用,属于中档题.

练习册系列答案
相关题目
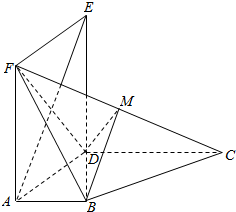 如图所示,平面ADEF⊥平面ABCD,且四边形ADEF为正方形,AD⊥DC,AB∥CD,AB=AD=$\frac{1}{2}$DC=2,M为CE的中点.
如图所示,平面ADEF⊥平面ABCD,且四边形ADEF为正方形,AD⊥DC,AB∥CD,AB=AD=$\frac{1}{2}$DC=2,M为CE的中点.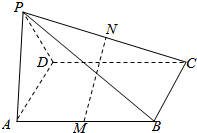 如图,四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点,且MN⊥PC,MN⊥AB.证明:平面PAD⊥平面PDC.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点,且MN⊥PC,MN⊥AB.证明:平面PAD⊥平面PDC.