题目内容
9.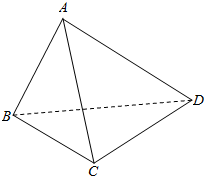 如图,已知三棱锥A-BCD中,△ABC与△ACD均为边长为2的正三角形,BD=$\sqrt{6}$,证明:面ABC⊥面ACD.
如图,已知三棱锥A-BCD中,△ABC与△ACD均为边长为2的正三角形,BD=$\sqrt{6}$,证明:面ABC⊥面ACD.
分析 取AC的中点E,连接BE,BD,由等边三角形的性质,结合勾股定理和线面垂直的判定,可得BE⊥平面ACD,再也面面垂直的判定定理,即可得证.
解答  证明:取AC的中点E,连接BE,BD,
证明:取AC的中点E,连接BE,BD,
由△ABC与△ACD均为边长为2的正三角形,
可得BE=DE=$\sqrt{3}$,BE⊥AC,DE⊥AC,
由BD=$\sqrt{6}$,BE2+DE2=BD2,
则BE⊥DE,
即有BE⊥平面ACD,
由BE?平面ACB,
则平面ACB⊥平面ACD.
点评 本题考查面面垂直的判定,考查空间线面的位置关系,考查推理能力,属于中档题.

练习册系列答案
相关题目
19.袋中有大小相同的红球6个,白球5个,从袋中每次任意取出1个球,直到取出的球是白球时为止,所需要的取球的次数为随机变量ξ,则ξ的可能值为( )
| A. | 1,2,…,6 | B. | 1,2,…,7 | C. | 1,2,…,11 | D. | 1,2,3… |
20.正方体的八个顶点中有四个恰好为正四面体的顶点,则正方体与正四面体的表面积的比值为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |
17.已知正四棱柱ABCD-A1B1C1D1中,对角线A1C=3,它的表面积是16,则它的体积是( )
| A. | 4 | B. | $\frac{112}{27}$ | C. | 4或$\frac{112}{27}$ | D. | $\frac{112}{9}$ |
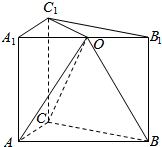 如图,在三棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为A1B1的中点O,且AC:BC:AB:AA1=1:1:$\sqrt{2}$:2.
如图,在三棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为A1B1的中点O,且AC:BC:AB:AA1=1:1:$\sqrt{2}$:2.