题目内容
19.已知四边形ABCD,$\overrightarrow{AB}$=$\overrightarrow{DC}$=(1,1),$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AD}}{|\overrightarrow{AD}|}$=$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$,则四边形ABCD的面积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 根据题意,利用向量加法的平行四边形法则得到四边形ABCD是菱形且∠BAD=120°,因此算出|$\overrightarrow{AB}$|=|$\overrightarrow{DC}$|=$\sqrt{2}$,即可求出四边形ABCD的面积.
解答 解:因为四边形ABCD,$\overrightarrow{AB}$=$\overrightarrow{DC}$,
所以四边形ABCD是平行四边形,
因为$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AD}}{|\overrightarrow{AD}|}$=$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$,
所以AC是平行四边形ABCD的角平分线,平行四边形为菱形,且∠BAD=120°,
根据$\overrightarrow{AB}$=(1,1)可得菱形的边长为$\sqrt{2}$.
因此四边形ABCD的面积S=$\sqrt{2}$×$\sqrt{2}$×sin60°=$\sqrt{3}$.
故选:C.
点评 本题给出四边形ABCD满足的向量等式,求四边形ABCD的面积.着重考查了向量加法的平行四边形法、向量模的公式与平行四边形面积求法等知识,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
14.函数y=2${\;}^{{x}^{2}}$(x∈R)满足( )
| A. | 在(-∞,+∞)上是增函数 | |
| B. | 在(-∞,+∞)上是减函数 | |
| C. | 在(-∞,0]上是增函数,在[0,+∞)上是减函数 | |
| D. | 在(-∞,0]上是减函数,在[0,+∞)上是增函数 |
7.设随机变量X服从正态分布N(3,4),则P(X<1-3a)=P(X>a2+7)成立的一个必要不充分条件是( )
| A. | a=1或2 | B. | a=±1或2 | C. | a=2 | D. | a=$\frac{3-\sqrt{5}}{2}$ |
4.下列说法中不正确的是( )
| A. | 随机变量ξ-N(3,σ2),若P(ξ>6)=0.3,则P(0<ξ<3)=0.2 | |
| B. | 如果一组数中每个数减去同一个非零常数,则这组数的平均数改变,方差不改变 | |
| C. | 对命题p:?x0∈R,使得x02-x0+1<0,¬p:?x∈R,有x2-x+1≥0 | |
| D. | 命题“在△ABC中,若sinA=sinB,则△ABC为等腰三角形”的否命题为真命题 |
8.若两个等差数列{an}、{bn}前n项和分别为An,Bn,且满足$\frac{{A}_{n}}{{B}_{n}}$=$\frac{4n+2}{5n-5}$,则$\frac{{a}_{4}+{a}_{14}}{{b}_{8}+{b}_{10}}$的值为( )
| A. | $\frac{7}{9}$ | B. | $\frac{7}{8}$ | C. | $\frac{19}{20}$ | D. | $\frac{8}{7}$ |
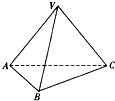 如图,三棱锥V-ABC的底面为正三角形,侧面VAC与底面垂直,且VA=VC,已知其侧(左)视图的面积为$\sqrt{3}$,其正(主)视图的面积为2.
如图,三棱锥V-ABC的底面为正三角形,侧面VAC与底面垂直,且VA=VC,已知其侧(左)视图的面积为$\sqrt{3}$,其正(主)视图的面积为2.