题目内容
7.设随机变量X服从正态分布N(3,4),则P(X<1-3a)=P(X>a2+7)成立的一个必要不充分条件是( )| A. | a=1或2 | B. | a=±1或2 | C. | a=2 | D. | a=$\frac{3-\sqrt{5}}{2}$ |
分析 根据充分条件和必要条件的定义,结合正态分布的性质,进行求解即可.
解答 解:若P(X<1-3a)=P(X>a2+7),
则1-3a与a2+7关于x=3对称,
则$\frac{1-3a+{a}^{2}+7}{2}$=3,
记记a2-3a+8=6,即a2-3a+2=0,
解得a=1或a=2,
则P(X<1-3a)=P(X>a2+7)成立的一个必要不充分条件是a=±1或2,
故选:B
点评 本题主要考查充分条件和必要条件的判断,以及正态分布的性质,根据正态分布的对称性是解决本题的关键.

练习册系列答案
相关题目
2.设集合P={-1,0,1},Q={x|$\sqrt{x}$<$\sqrt{2}$},则P∩Q=( )
| A. | {0,1} | B. | {1} | C. | {0} | D. | {-1,0,1} |
19.已知四边形ABCD,$\overrightarrow{AB}$=$\overrightarrow{DC}$=(1,1),$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AD}}{|\overrightarrow{AD}|}$=$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$,则四边形ABCD的面积为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
16.已知△ABC的三个顶点ABC及所在平面内一点,P满足$\overrightarrow{PA}$+$\overrightarrow{PB}$+2$\overrightarrow{PC}$=$\overrightarrow{CB}$,则点P与△ABC的关系为( )
| A. | P在△ABC内部 | B. | P在AB边所在直线上 | ||
| C. | P在BC边所在直线上 | D. | P在AC边所在直线上 |
17.小王有70元钱,现有面值分别为20元和30元的两种IC电话卡,若他至少买一张,则不同的买法共用( )
| A. | 7种 | B. | 8种 | C. | 6种 | D. | 9种 |
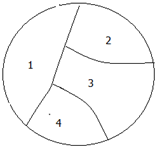 用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.
用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.