题目内容
4.下列说法中不正确的是( )| A. | 随机变量ξ-N(3,σ2),若P(ξ>6)=0.3,则P(0<ξ<3)=0.2 | |
| B. | 如果一组数中每个数减去同一个非零常数,则这组数的平均数改变,方差不改变 | |
| C. | 对命题p:?x0∈R,使得x02-x0+1<0,¬p:?x∈R,有x2-x+1≥0 | |
| D. | 命题“在△ABC中,若sinA=sinB,则△ABC为等腰三角形”的否命题为真命题 |
分析 A.随机变量ξ服从正态分布N(3,σ2),得到曲线关于x=3对称,根据曲线的对称性得到小于0的和大于6的概率是相等的,从而得到结果;
B.根据平均数和方差的特点知正确;
C.利用命题的否定,可得结论;
D.写出否命题,即可判断.
解答 解:对于A,随机变量ξ服从正态分布N(3,σ2),∴曲线关于x=3对称,∴P(0<ξ<3)=0.2,故正确;
对于B,如果一组数中每个数减去同一个非零常数,则这一组数的平均数改变,方差不改变,故正确;
对于C,对命题p:?x0∈R,使得x02-x0+1<0,¬p:?x∈R,有x2-x+1≥0,故正确;
对于D,命题“在△ABC中,若sinA=sinB,则△ABC为等腰三角形”的否命题是“在△ABC中,若sinA≠sinB,则△ABC不为等腰三角形”是假命题,故不正确;
故选:D.
点评 本题考查众数,中位数,平均数和方差,本题解题的关键是理解这几个特征数的特点与求法,本题是一个基础题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
19.已知四边形ABCD,$\overrightarrow{AB}$=$\overrightarrow{DC}$=(1,1),$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AD}}{|\overrightarrow{AD}|}$=$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$,则四边形ABCD的面积为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
16.已知△ABC的三个顶点ABC及所在平面内一点,P满足$\overrightarrow{PA}$+$\overrightarrow{PB}$+2$\overrightarrow{PC}$=$\overrightarrow{CB}$,则点P与△ABC的关系为( )
| A. | P在△ABC内部 | B. | P在AB边所在直线上 | ||
| C. | P在BC边所在直线上 | D. | P在AC边所在直线上 |
14.已知点P(x,y)是函数y=$\sqrt{-{x}^{2}+4x-3}$上的点,则$\frac{y+1}{x}$的取值范围是( )
| A. | (-∞,1] | B. | (-∞,$\frac{1}{3}$] | C. | (-∞,$\frac{1}{3}$]∪[1,+∞) | D. | [$\frac{1}{3}$,$\frac{4}{3}$] |
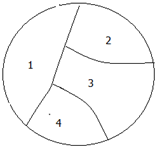 用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.
用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.