题目内容
4.函数y=$\frac{1}{2}$x2-lnx的单调递减区间为( )| A. | (-1,1) | B. | [1,+∞) | C. | (0,+∞) | D. | (0,1] |
分析 对函数y=$\frac{1}{2}$x2-lnx求导,利用y′≤0,求出函数y的单调递减区间即可.
解答 解:∵函数y=$\frac{1}{2}$x2-lnx,x>0,
∴y′=x-$\frac{1}{x}$=$\frac{{x}^{2}-1}{x}$,
令y′≤0,
即x2-1≤0,
解得-1≤x≤1;
综上,0<x≤1,
∴函数y的单调递减区间为(0,1].
故选:D.
点评 本题考查了利用导数判断函数的单调性问题,也考查了对数函数性质的应用问题,是基础题目.

练习册系列答案
相关题目
15.过抛物线y2=4x的焦点作一条直线与抛物线相交于A,B两点,它们到直线x=-2的距离之和等于7,则这样的直线( )
| A. | 有无穷多条 | B. | 有且仅有一条 | C. | 有且仅有两条 | D. | 不存在 |
12.抛物线x2=8y的准线方程是( )
| A. | x=$\frac{1}{32}$ | B. | y=2 | C. | y=$\frac{1}{32}$ | D. | y=-2 |
19.抛物线C:y2=2px(p>0)的焦点为F,准线l与x轴交于点A,抛物线C上一点M满足MF⊥x轴,且S△AFM=8,则抛物线C的方程为( )
| A. | y2=2x | B. | y2=4x | C. | y2=8x | D. | y2=16x |
9.函数f(x)=(x-2)ex的单调递增区间是( )
| A. | (-∞,1) | B. | ( 0,2 ) | C. | (1,+∞) | D. | (2,+∞) |
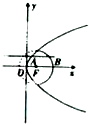 如图,直线y=m与抛物线y2=4x交于点A,与圆(x-1)2+y2=4的实线部分交于点B,F为抛物线的焦点,则三角形ABF的周长的取值范围是(4,6).
如图,直线y=m与抛物线y2=4x交于点A,与圆(x-1)2+y2=4的实线部分交于点B,F为抛物线的焦点,则三角形ABF的周长的取值范围是(4,6).