题目内容
16.已知抛物线C:y2=2px(p>0)的焦点为F并且经过点A(1,-2).(1)求抛物线C的方程;
(2)过F作倾斜角为45°的直线l,交抛物线C于M,N两点,O为坐标原点,求△OMN的面积.
分析 (1)把点A(1,-2)代入抛物线C:y2=2px(p>0),解得p即可得出.
(2)F(1,0).设M(x1,y1),N(x2,y2).直线l的方程为:y=x-1.与抛物线方程联立可得根与系数的关系,利用弦长公式可得:|MN|=$\sqrt{2[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$.利用点到直线的距离公式可得:原点O到直线MN的距离d.利用△OMN的面积S=$\frac{1}{2}|MN|•d$即可得出.
解答 解:(1)把点A(1,-2)代入抛物线C:y2=2px(p>0),可得(-2)2=2p×1,解得p=2.
∴抛物线C的方程为:y2=4x.
(2)F(1,0).
设M(x1,y1),N(x2,y2).
直线l的方程为:y=x-1.
联立$\left\{\begin{array}{l}{y=x-1}\\{{y}^{2}=4x}\end{array}\right.$,
化为x2-6x+1=0,
∴x1+x2=6,x1x2=1.
∴|MN|=$\sqrt{2[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{2({6}^{2}-4)}$=8.
原点O到直线MN的距离d=$\frac{1}{\sqrt{2}}$.
∴△OMN的面积S=$\frac{1}{2}|MN|•d$=$\frac{1}{2}×8×\frac{1}{\sqrt{2}}$=2$\sqrt{2}$.
点评 本题考查了抛物线的标准方程及其性质、直线与抛物线相交问题转化为方程联立可得根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.已知抛物线C:y2=2px的焦点为F,过其焦点且斜率为1的直线交抛物线于M、N两点,若线段MN中点纵坐标为4,则该抛物线准线方程为( )
| A. | x=1 | B. | x=-1 | C. | x=2 | D. | x=-2 |
4.函数y=$\frac{1}{2}$x2-lnx的单调递减区间为( )
| A. | (-1,1) | B. | [1,+∞) | C. | (0,+∞) | D. | (0,1] |
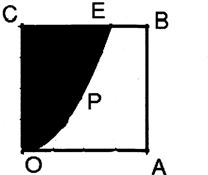 如图,某工业园区有一边长为2(单位:千米)的正方形地块OABC,其中OCE(阴影部分)是一个已建工厂,计划在地块OABC内修一条与曲边OE相切的直路l(宽度不计),切点为P,直线l把该地块分为两部分,已知曲线段OE是以点O为顶点,OC为对称轴且开口向上的抛物线的一段,CE=$\sqrt{2}$.
如图,某工业园区有一边长为2(单位:千米)的正方形地块OABC,其中OCE(阴影部分)是一个已建工厂,计划在地块OABC内修一条与曲边OE相切的直路l(宽度不计),切点为P,直线l把该地块分为两部分,已知曲线段OE是以点O为顶点,OC为对称轴且开口向上的抛物线的一段,CE=$\sqrt{2}$.