题目内容
19.抛物线C:y2=2px(p>0)的焦点为F,准线l与x轴交于点A,抛物线C上一点M满足MF⊥x轴,且S△AFM=8,则抛物线C的方程为( )| A. | y2=2x | B. | y2=4x | C. | y2=8x | D. | y2=16x |
分析 求出抛物线的焦点和准线方程,令x=$\frac{p}{2}$,求得|MF|,再由三角形的面积公式计算可得p=4,进而得到抛物线的方程.
解答 解:抛物线C:y2=2px(p>0)的焦点为F($\frac{p}{2}$,0),准线l:x=-$\frac{p}{2}$,
则|AF|=p,
由MF⊥x轴,令x=$\frac{p}{2}$,可得y2=p2,解得y=±p,
则S△AFM=$\frac{1}{2}$•|AF|•|MF|=$\frac{1}{2}$p2=8,
解得p=4.
即有抛物线方程为y2=8x,
故选C.
点评 本题考查抛物线的方程和性质,主要考查准线方程和焦点坐标,同时考查三角形的面积计算,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.已知抛物线C:y2=2px的焦点为F,过其焦点且斜率为1的直线交抛物线于M、N两点,若线段MN中点纵坐标为4,则该抛物线准线方程为( )
| A. | x=1 | B. | x=-1 | C. | x=2 | D. | x=-2 |
4.函数y=$\frac{1}{2}$x2-lnx的单调递减区间为( )
| A. | (-1,1) | B. | [1,+∞) | C. | (0,+∞) | D. | (0,1] |
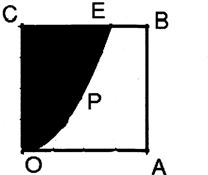 如图,某工业园区有一边长为2(单位:千米)的正方形地块OABC,其中OCE(阴影部分)是一个已建工厂,计划在地块OABC内修一条与曲边OE相切的直路l(宽度不计),切点为P,直线l把该地块分为两部分,已知曲线段OE是以点O为顶点,OC为对称轴且开口向上的抛物线的一段,CE=$\sqrt{2}$.
如图,某工业园区有一边长为2(单位:千米)的正方形地块OABC,其中OCE(阴影部分)是一个已建工厂,计划在地块OABC内修一条与曲边OE相切的直路l(宽度不计),切点为P,直线l把该地块分为两部分,已知曲线段OE是以点O为顶点,OC为对称轴且开口向上的抛物线的一段,CE=$\sqrt{2}$.