题目内容
定义在区间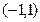 上的函数f (x)满足:对任意的
上的函数f (x)满足:对任意的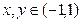 ,
,
都有 . 求证f (x)为奇函数;
. 求证f (x)为奇函数;
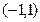 上的函数f (x)满足:对任意的
上的函数f (x)满足:对任意的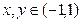 ,
,都有
 . 求证f (x)为奇函数;
. 求证f (x)为奇函数;证明略
欲证明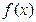 为奇函数,就要证明
为奇函数,就要证明 ,但这是抽象函数,应设法充
,但这是抽象函数,应设法充
分利用条件“对任意的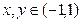 ,都有
,都有 ”中的
”中的 进行合理
进行合理
“赋值”
令x = y = 0,则
f (0) + f (0) =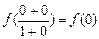
∴ f (0) = 0
令x∈(-1, 1) ∴-x∈(-1, 1)
∴ f (x) + f (-x) = f ( ) = f (0) = 0
) = f (0) = 0
∴ f (-x) =-f (x)
∴ f (x) 在(-1,1)上为奇函数
对于抽象函数的奇偶性问题,解决的关键是巧妙进行“赋值”,而抽象函数的不等式问题,要灵活利用已知条件,尤其是f (x1) -f (x2) = f (x1) + f (-x2)
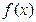 为奇函数,就要证明
为奇函数,就要证明 ,但这是抽象函数,应设法充
,但这是抽象函数,应设法充分利用条件“对任意的
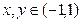 ,都有
,都有 ”中的
”中的 进行合理
进行合理“赋值”
令x = y = 0,则
f (0) + f (0) =
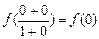
∴ f (0) = 0
令x∈(-1, 1) ∴-x∈(-1, 1)
∴ f (x) + f (-x) = f (
 ) = f (0) = 0
) = f (0) = 0∴ f (-x) =-f (x)
∴ f (x) 在(-1,1)上为奇函数
对于抽象函数的奇偶性问题,解决的关键是巧妙进行“赋值”,而抽象函数的不等式问题,要灵活利用已知条件,尤其是f (x1) -f (x2) = f (x1) + f (-x2)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
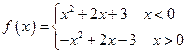 ,判断
,判断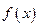 的奇偶性,并加以证明.
的奇偶性,并加以证明.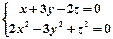 ,则方程组的解(x,y,z)= 。
,则方程组的解(x,y,z)= 。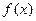 是定义在
是定义在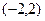 上的减函数,若
上的减函数,若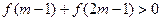 ,求实数
,求实数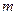 的取值范围。
的取值范围。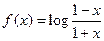 ,
,  为偶函数,则
为偶函数,则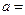 .
.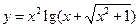 的奇偶性 .
的奇偶性 .