题目内容
(本小题满分12分)已知函数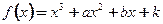 满足
满足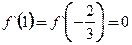 ,
,
(Ⅰ)求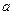 、
、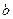 的值及函数
的值及函数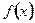 的单调递增区间;
的单调递增区间;
(Ⅱ)若对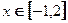 ,不等式
,不等式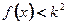 恒成立,求
恒成立,求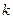 的取值范围。
的取值范围。
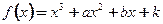 满足
满足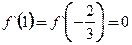 ,
,(Ⅰ)求
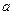 、
、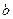 的值及函数
的值及函数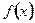 的单调递增区间;
的单调递增区间;(Ⅱ)若对
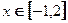 ,不等式
,不等式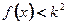 恒成立,求
恒成立,求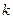 的取值范围。
的取值范围。(Ⅰ) 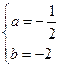 ,
, 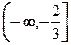 ,
,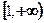 。(Ⅱ)
。(Ⅱ) 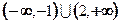
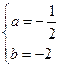 ,
, 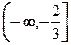 ,
,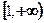 。(Ⅱ)
。(Ⅱ) 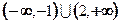
:(Ⅰ)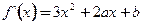 ,由
,由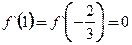 得
得

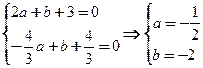
∴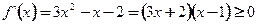 ,故
,故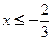 或
或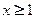
故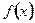 的单调递增区间为
的单调递增区间为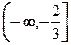 ,
,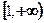 。
。
(Ⅱ)法1:当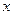 变化时,
变化时,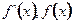 的变化情况如下表
的变化情况如下表
可见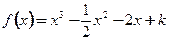 ,
,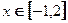 ,当
,当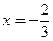 时,
时,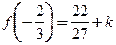 为极大值,而
为极大值,而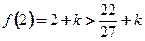 ,则
,则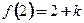 为最大值,故要使不等式
为最大值,故要使不等式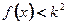 在
在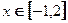 时恒成立,只须
时恒成立,只须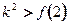 ,即
,即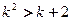
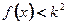 即
即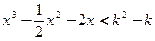
解得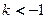 或
或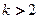
∴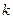 的取值范围为
的取值范围为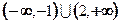 。
。
法2:由(Ⅰ)得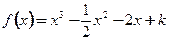
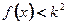 即
即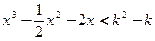
对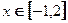 ,不等式
,不等式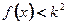 恒成立,即
恒成立,即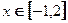 不等式
不等式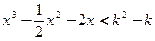 恒成立,
恒成立,
构造函数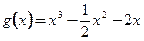 ,只须
,只须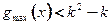
∵ ,令
,令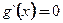 得
得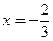 和
和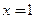
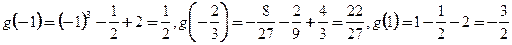
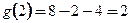
∴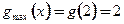 ,解不等式
,解不等式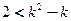 得
得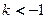 或
或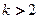
∴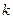 的取值范围为
的取值范围为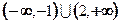 。
。
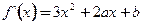 ,由
,由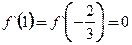 得
得
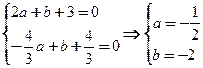
∴
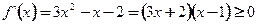 ,故
,故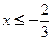 或
或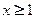
故
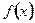 的单调递增区间为
的单调递增区间为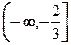 ,
,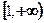 。
。(Ⅱ)法1:当
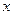 变化时,
变化时,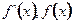 的变化情况如下表
的变化情况如下表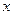 | 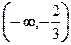 | 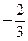 | 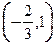 | 1 | 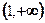 |
 | + | 0 | - | 0 | + |
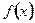 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
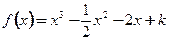 ,
,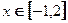 ,当
,当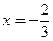 时,
时,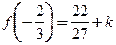 为极大值,而
为极大值,而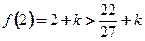 ,则
,则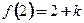 为最大值,故要使不等式
为最大值,故要使不等式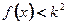 在
在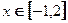 时恒成立,只须
时恒成立,只须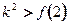 ,即
,即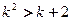
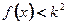 即
即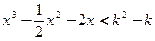
解得
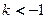 或
或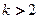
∴
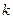 的取值范围为
的取值范围为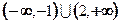 。
。法2:由(Ⅰ)得
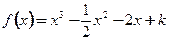
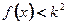 即
即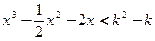
对
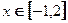 ,不等式
,不等式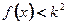 恒成立,即
恒成立,即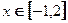 不等式
不等式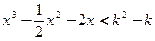 恒成立,
恒成立,构造函数
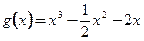 ,只须
,只须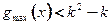
∵
 ,令
,令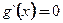 得
得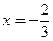 和
和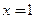
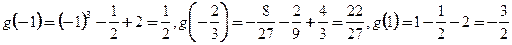
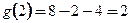
∴
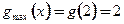 ,解不等式
,解不等式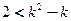 得
得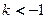 或
或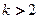
∴
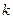 的取值范围为
的取值范围为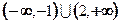 。
。
练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
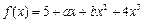 在
在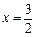 及
及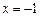 处有极值,
处有极值,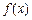 的极值;
的极值;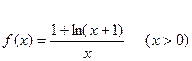 ,
,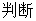
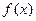 在区间
在区间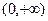 是增函数还是减函数?并证明你的结论;
是增函数还是减函数?并证明你的结论;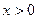 时,
时,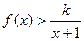 恒成立,求整数
恒成立,求整数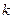 的最小值。
的最小值。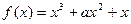 ,
,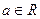 是常数,
是常数,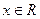 .
.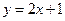 是曲线
是曲线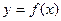 的一条切线,求
的一条切线,求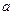 的值;
的值;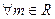 ,试证明
,试证明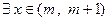 ,使
,使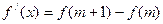 .
.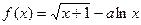 (
(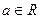 )
)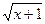
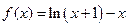 ,(1)求函数
,(1)求函数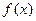 的单调减区间;(2)若
的单调减区间;(2)若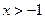 ,证明:
,证明: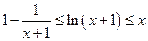 。
。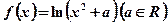 . (1)求在函数
. (1)求在函数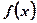 图像上点
图像上点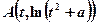 处的切线
处的切线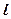 的方程;(2)若切线
的方程;(2)若切线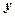 轴上的纵坐标截距记为
轴上的纵坐标截距记为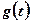 ,讨论
,讨论