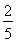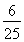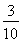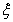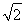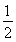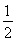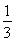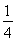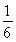题目内容
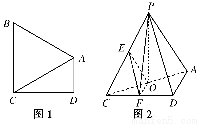
已知双曲线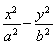
＝1(a＞0，b＞0)的左、右焦点分别为F1，F2，点O为双曲线的中心，点P在双曲线右支上，△PF1F2内切圆的圆心为Q，圆Q与x轴相切于点A，过F2作直线PQ的垂线，垂足为B，则下列结论成立的是( )
A．|OA|＞|OB| B．|OA|＜|OB|
C．|OA|＝|OB| D．|OA|与|OB|大小关系不确定
C
【解析】由于点Q为三角形PF1F2内切圆的圆心，故过点F2作PQ的垂线并延长交PF1于点N，易知垂足B为F2N的中点，连接OB，则|OB|＝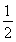
|F1N|＝
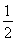(|F1P|－|F2P|)＝a，又设内切圆与PF1，PF2分别切于G，H，则由内切圆性质可得|PG|＝|PH|，|F1G|＝|F1A|，|F2A|＝|F2H|，故|F1P|－|F2P|＝|F1A|－|F2A|＝2a，设|OA|＝x，则有x＋c－(c－x)＝2a，解得|OA|＝a，故有|OA|＝|OB|＝a，故选C.
练习册系列答案
相关题目
某车间将10名技工平均分成甲、乙两组加工某种零件，在单位时间内每个技工加工的合格零件数如下表：
| 1号 | 2号 | 3号 | 4号 | 5号 |
甲组 | 4 | 5 | x | 9 | 10 |
乙组 | 5 | 6 | 7 | y | 9 |
(1)已知两组技工在单位时间内加工的合格零件平均数为7，分别求出甲、乙两组技工在单位时间内加工的合格零件的方差，并由此分析两组技工的加工水平；
(2)质检部门从该车间甲、乙两组中各随机抽取一名技工，对其加工的零件进行检测，若2人加工的合格零件个数之和超过14，则称该车间“质量合格”，求该车间“质量合格”的概率．
