题目内容
【题目】在党的群众教育路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对单位的各项开展工作进行打分评价,现获得如下数据:70,82,81,76,84,80,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,74,86,79,76.
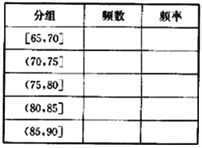
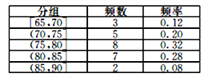
(1)根据上述数据完成样本的频率分布表;
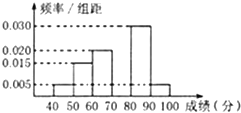
(2)根据(1)的频率分布表,完成样本分布直方图;

(3)从区间![]() 和
和![]() 中任意抽取两个评分,求两个评分来自不同区间的概率.
中任意抽取两个评分,求两个评分来自不同区间的概率.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】试题分析:
(1)从已给数据可得各组频数,从而得频率,频率分布表既得;(1)由频率分布表可得频率分布直方图;(3)在区间![]() 内有三人编号为
内有三人编号为![]() ,在区间
,在区间![]() 上有2人,编号为
上有2人,编号为![]() ,可用列举法得出任选2人的所有情形,从而得出符合条件的事件数,由古典概型概率公式可得概率.
,可用列举法得出任选2人的所有情形,从而得出符合条件的事件数,由古典概型概率公式可得概率.
试题解析:
(1)
(2)样本频率分布直方图为
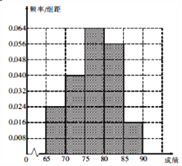
(3)设在![]() 内的3个评分为
内的3个评分为![]() ,
, ![]() 内的2个评分为
内的2个评分为![]() ,则所有的抽法有
,则所有的抽法有![]() 共计10种,而两个评分来自不同区间的有6种,所以两个评分来自不同区间的概率为
共计10种,而两个评分来自不同区间的有6种,所以两个评分来自不同区间的概率为![]() .
.

【题目】当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,并制成下面的![]() 列联表:
列联表:
及格 | 不及格 | 合计 | |
很少使用手机 | 20 | 6 | 26 |
经常使用手机 | 10 | 14 | 24 |
合计 | 30 | 20 | 50 |
(1)判断是否有![]() 的把握认为经常使用手机对学习成绩有影响?
的把握认为经常使用手机对学习成绩有影响?
(2)从这50人中,选取一名很少使用手机的同学记为甲和一名经常使用手机的同学记为乙,解一道数学题,甲、乙独立解出此题的概率分别为![]() ,且
,且![]() ,若
,若![]() ,则此二人适合结为学习上互帮互助的“学习师徒”,记
,则此二人适合结为学习上互帮互助的“学习师徒”,记![]() 为两人中解出此题的人数,若
为两人中解出此题的人数,若![]() 的数学期望
的数学期望![]() ,问两人是否适合结为“学习师徒”?
,问两人是否适合结为“学习师徒”?
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
参考公式及数据: 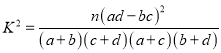 ,其中
,其中![]() .
.