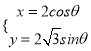题目内容
【题目】当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,并制成下面的![]() 列联表:
列联表:
及格 | 不及格 | 合计 | |
很少使用手机 | 20 | 6 | 26 |
经常使用手机 | 10 | 14 | 24 |
合计 | 30 | 20 | 50 |
(1)判断是否有![]() 的把握认为经常使用手机对学习成绩有影响?
的把握认为经常使用手机对学习成绩有影响?
(2)从这50人中,选取一名很少使用手机的同学记为甲和一名经常使用手机的同学记为乙,解一道数学题,甲、乙独立解出此题的概率分别为![]() ,且
,且![]() ,若
,若![]() ,则此二人适合结为学习上互帮互助的“学习师徒”,记
,则此二人适合结为学习上互帮互助的“学习师徒”,记![]() 为两人中解出此题的人数,若
为两人中解出此题的人数,若![]() 的数学期望
的数学期望![]() ,问两人是否适合结为“学习师徒”?
,问两人是否适合结为“学习师徒”?
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
参考公式及数据: 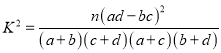 ,其中
,其中![]() .
.
【答案】(1)有把握(2)适合
【解析】试题分析:(1)由列联表可求出常数![]() 的值,结合所给数据,利用独立性检验可得出有
的值,结合所给数据,利用独立性检验可得出有![]() 的把握得出结果;(2)由题写出
的把握得出结果;(2)由题写出![]() 的所有可能取值,并列出其概率,写出分布列,计算出期望值,利用所给数据得出方程,解方程可得具体概率值,再利用条件可判断是否适合结为师徒.
的所有可能取值,并列出其概率,写出分布列,计算出期望值,利用所给数据得出方程,解方程可得具体概率值,再利用条件可判断是否适合结为师徒.
试题解析:(1)由列联表可得: ![]()
![]() ,
,
所以,有![]() 的把握认为经常使用手机对学习成绩有影响.
的把握认为经常使用手机对学习成绩有影响.
(2)依题:解出此题的人数![]() 可能取值为0,1,2,可得分布列为
可能取值为0,1,2,可得分布列为
| 0 | 1 | 2 |
|
|
|
|
所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
且![]() ,
,
所以二人适合结为“学习师徒”.

【题目】为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了1000名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合计 | |
男大学生 | 610 | ||
女大学生 | 90 | ||
合计 | 800 |
(1) 根据题意完成表格;
(2) 是否有![]() 的把握认为愿意做志愿者工作与性别有关?
的把握认为愿意做志愿者工作与性别有关?
参考公式及数据: 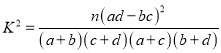 ,其中
,其中![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【题目】学校射击队的某一选手射击一次,其命中环数的概率如表:
命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求该选手射击一次,
(1)命中9环或10环的概率.
(2)至少命中8环的概率.
(3)命中不足8环的概率.
【题目】某项科研活动共进行了5次试验,其数据如下表所示:
特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 555 | 559 | 551 | 563 | 552 |
| 601 | 605 | 597 | 599 | 598 |
(1)从5次特征量![]() 的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
(2)求特征量![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并预测当特征量
;并预测当特征量![]() 为570时特征量
为570时特征量![]() 的值.
的值.
(附:回归直线的斜率和截距的最小二乘法估计公式分别为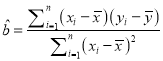 ,
, ![]() )
)