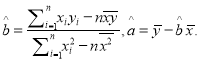题目内容
【题目】已知函数![]() .若
.若![]() 时方程
时方程![]() 有两 个不同的实根,则实数
有两 个不同的实根,则实数![]() 的取值范围是________;若
的取值范围是________;若![]() 的值域为
的值域为![]() ,则实数
,则实数![]() 的
的
取值范围是________.
【答案】 ![]()
![]()
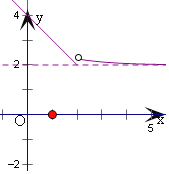
【解析】作出![]() 的图象,
的图象,
由a=![]() 时方程f(x)=b有两个不同的实根,
时方程f(x)=b有两个不同的实根,
可得b>2,且b<2+0.52=![]() ,
,
即有b∈(2, ![]() );
);
函数![]() ,
,
当0<a<1时,x2时,f(x)=4x2,
x>2时,f(x)=ax+2a+1递减,
可得2a+1<f(x)<a2+2a+1,
f(x)的值域为[2,+∞),可得2a+12,解得![]() a<1;
a<1;
当a>1时,x2时,f(x)=4x2,
x>2时,f(x)=ax+2a+1递增,
可得f(x)>a2+2a+1>4,
则f(x)的值域为[2,+∞)成立,a>1恒成立。
综上可得a∈[![]() ,1)∪(1,+∞).
,1)∪(1,+∞).

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
【题目】某项科研活动共进行了5次试验,其数据如下表所示:
特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 555 | 559 | 551 | 563 | 552 |
| 601 | 605 | 597 | 599 | 598 |
(1)从5次特征量![]() 的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
(2)求特征量![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并预测当特征量
;并预测当特征量![]() 为570时特征量
为570时特征量![]() 的值.
的值.
(附:回归直线的斜率和截距的最小二乘法估计公式分别为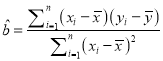 ,
, ![]() )
)