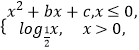题目内容
【题目】已知数列{an]的前n项和记为Sn , 且满足Sn=2an﹣n,n∈N* (Ⅰ)求数列{an}的通项公式;
(Ⅱ)证明: ![]() +…
+… ![]() (n∈N*)
(n∈N*)
【答案】解:(Ⅰ)∵Sn=2an﹣n(n∈N+),
∴Sn﹣1=2an﹣1﹣n+1=0(n≥2),
两式相减得:an=2an﹣1+1,
变形可得:an+1=2(an﹣1+1),
又∵a1=2a1﹣1,即a1=1,
∴数列{an+1}是首项为2、公比为2的等比数列,
∴an+1=22n﹣1=2n,an=2n﹣1.
(Ⅱ)由 ![]() ,(k=1,2,…n),
,(k=1,2,…n),
∴ ![]() =
= ![]() ,
,
由 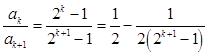 =
= ![]() ﹣
﹣ ![]() ,(k=1,2,…n),
,(k=1,2,…n),
得 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
综上, ![]() +…
+… ![]() (n∈N*)
(n∈N*)
【解析】(Ⅰ)通过Sn=2an﹣n(n∈N+)与Sn﹣1=2an﹣1﹣(n﹣1)(n≥2)作差、变形可知an+1=2(an﹣1+1),进而计算即得结论.(Ⅱ)利用 ![]() ,(k=1,2,…n),
,(k=1,2,…n), ![]() =
= ![]() ﹣
﹣ ![]() (k=1,2,…n),可证明,
(k=1,2,…n),可证明, ![]() +…
+… ![]() (n∈N*).
(n∈N*).

练习册系列答案
相关题目