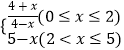题目内容
【题目】已知向量 ![]() ,
, ![]() ,函数
,函数 ![]() ,
, ![]() .
.
(1)若 ![]() 的最小值为-1,求实数
的最小值为-1,求实数 ![]() 的值;
的值;
(2)是否存在实数 ![]() ,使函数
,使函数 ![]() ,
, ![]() 有四个不同的零点?若存在,求出
有四个不同的零点?若存在,求出 ![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】
(1)解:∵ ![]() ,
,
![]() ,
,
∴ ![]()
![]() ,
,
∵ ![]() ∴
∴ ![]() ,
,
![]()
![]() ,令
,令 ![]() ,
,
∴ ![]()
∵ ![]() ,对称轴为
,对称轴为 ![]() ,
,
①当 ![]() 即
即 ![]() 时,当
时,当 ![]() 时,
时, ![]() ∴
∴ ![]() 舍,
舍,
②当 ![]() 即
即 ![]() 时,当
时,当 ![]() 时,
时, ![]() ∴
∴ ![]() ,
,
③当 ![]() 即
即 ![]() 是,当
是,当 ![]() 时,
时, ![]() ∴
∴ ![]() 舍,
舍,
综上, ![]() .
.
(2)解:令 ![]() ,即
,即 ![]() ,
,
∴ ![]() 或
或 ![]() ,
,
∵ ![]() ,
, ![]() 有四个不同的零点,
有四个不同的零点,
∴方程 ![]() 和
和 ![]() 在
在 ![]() 上共有四个不同的实根,
上共有四个不同的实根,
∴ 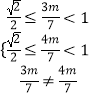 ∴
∴ 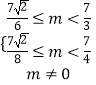 ∴
∴ ![]() .
.
【解析】(1)根据向量的数量积坐标运算公式结合两角和差的正弦公式整理原式可得![]() =cos2x,再结合向量坐标的线性运算求出
=cos2x,再结合向量坐标的线性运算求出![]() 的坐标,进而求出其模的值,然后得出f(x) 的代数式f ( x ) = cos 2 x 2 m cos x + 1 = 2 cos2 x 2 m cos x,令 t = cos x由角的取值范围得出t的取值范围t∈ [
的坐标,进而求出其模的值,然后得出f(x) 的代数式f ( x ) = cos 2 x 2 m cos x + 1 = 2 cos2 x 2 m cos x,令 t = cos x由角的取值范围得出t的取值范围t∈ [ ![]() , 1 ] ,根据二次函数在指定区间上的最值 ymin = 1 得出对称轴 t =
, 1 ] ,根据二次函数在指定区间上的最值 ymin = 1 得出对称轴 t = ![]() ,分类讨论求解得出m的值。(2)利用(1)的结论求出 g(x) 的解析式求出cosx的值,令函数y=cosx再区间有四个不同的零点,利用函数与方程的关系,将实根转化为函数与直线的交点问题求解即可。
,分类讨论求解得出m的值。(2)利用(1)的结论求出 g(x) 的解析式求出cosx的值,令函数y=cosx再区间有四个不同的零点,利用函数与方程的关系,将实根转化为函数与直线的交点问题求解即可。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目