Question

【题目】已知椭圆C： 的上顶点M与左、右焦点F1、F2构成三角形MF1F2面积为 ，又椭圆C的离心率为 ．
（1）求椭圆C的方程；
（2）椭圆C的下顶点为N，过点T（t，2）（t≠0）的直线TM，TN分别与椭圆C交于E，F两点．若△TMN的面积是△TEF的面积的k倍，求k的最大值．

Answer 1

【答案】
（1）解：椭圆离心率e= = ，

又 ，a2=b2+c2，

解得a=2，b=1，

∴椭圆C的方程为

（2）解：∵S△TMN= |MN||t|=|t|，

直线TM的方程为：y= ，

联立 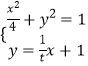，得 ，

∴E（ ， ），

直线TN的方程为：y= ，

联立 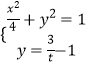，得 ，

∴F（ ， ），

∵E到直线TN：3x﹣ty﹣t=0的距离：

d= = ，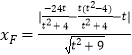

TF=

=

=

= ，

∴S△TEF= = = ，

∴S△TEF= = = ，

∴k= = ，

令t2+12=n＞12，则k= =1+ ≤ ，

当且仅当n=24，即t= 时，等号成立，

∴k的最大值为

【解析】（1）由椭圆的上顶点M与左、右焦点构成三角形面积为 ，离心率为 ，求出a，b，由此能求出椭圆C的方程．（2）S△TMN= |MN||t|=|t|，直线TM的方程为：y= ，直线TN的方程为：y= ，求出E、F、E到直线TN：3x﹣ty﹣t=0的距离和TF，从而得到k= = ，由此能求出k的最大值．