题目内容
设无穷等差数列{an}的前n项和为Sn.
(Ⅰ)若首项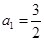 ,公差
,公差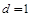 ,求满足
,求满足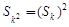 的正整数k;
的正整数k;
(Ⅱ)求所有的无穷等差数列{an},使得对于一切正整数k都有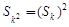 成立
成立
(Ⅰ)若首项
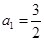 ,公差
,公差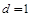 ,求满足
,求满足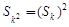 的正整数k;
的正整数k;(Ⅱ)求所有的无穷等差数列{an},使得对于一切正整数k都有
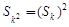 成立
成立(Ⅰ)  (Ⅱ)见解析
(Ⅱ)见解析
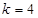 (Ⅱ)见解析
(Ⅱ)见解析【错解分析】本小题主要考查数列的基本知识,以及运用数学知识分析和解决问题的能力.学生在解第(Ⅱ)时极易根据条件“对于一切正整数k都有
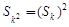 成立”这句话将k取两个特殊值确定出等差数列的首项和公差,但没有认识到求解出的等差数列仅是对已知条件成立的必要条件,但不是条件成立的充分条件。还应进一步的由特殊到一般。
成立”这句话将k取两个特殊值确定出等差数列的首项和公差,但没有认识到求解出的等差数列仅是对已知条件成立的必要条件,但不是条件成立的充分条件。还应进一步的由特殊到一般。【正解】解:(I)当
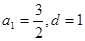 时
时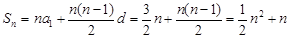
由
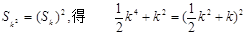 ,即
,即 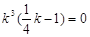 又
又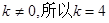 .
.(II)设数列{an}的公差为d,则在
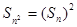 中分别取k=1,2,得
中分别取k=1,2,得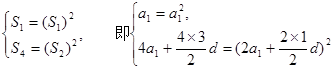
由(1)得
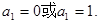 当
当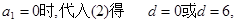
若
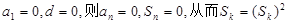 成立 ,
成立 ,若
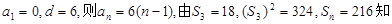
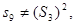 故所
故所数列不符合题意.当

若
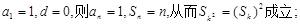
若
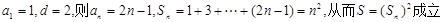 .
.综上,共有3个满足条件的无穷等差数列:
①{an} : an=0,即0,0,0,…;②{an} : an=1,即1,1,1,…; ③{an} : an=2n-1,即1,3,5,…,

练习册系列答案
相关题目
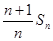
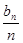 的最小值.
的最小值.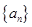 中,如果
中,如果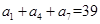 ,
,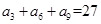 ,数列
,数列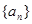 的前
的前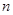 项和为
项和为 ,若
,若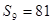 ,则
,则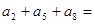
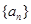 满足
满足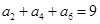 ,则
,则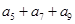 的值等于 。
的值等于 。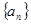 中,
中,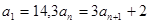 ,则使
,则使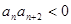 成立的
成立的 值是( )
值是( )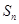 是等差数列
是等差数列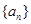 的前n项和,
的前n项和,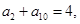 则
则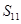 的值为( )
的值为( )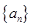 是等差数列,
是等差数列,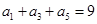 ,
,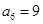 ,则这个数列的前6项和等于( )
,则这个数列的前6项和等于( )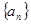 中,
中,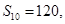 那么
那么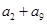 的值是( )
的值是( )