题目内容

8．下列求导运算正确的是（　　）
A．（x+$\frac{1}{x}$）′=1+$\frac{1}{{x}^{2}}$B．（3x）′=3xlog3e
C．（log23x）′=$\frac{1}{xln2}$D．（x2cos x）′=-2xsin x

分析 根据导数的运算法则求导即可．

解答 解：（x+$\frac{1}{x}$）′=1-$\frac{1}{{x}^{2}}$，
（3x）′=3xln3，
（log23x）′=（log23+log2x）′=$\frac{1}{xln2}$，
（x2cos x）′=2xcosx-x2sinx，
故选：C．

点评 本题考查了导数的运算法则，和常用函数的导数公式，属于基础题．

练习册系列答案
相关题目
18．某几何体的三视图，如图所示，则该几何体的体积为（　　）
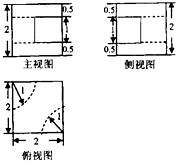
A．8-$\frac{π}{6}$B．8-$\frac{π}{4}$C．8-$\frac{π}{3}$D．8-$\frac{π}{2}$
19．已知函数f（x）=$\frac{{{2^x}-1}}{{{2^x}+1}}$，g（x）=x2+2mx+$\frac{5}{3}$
（1）用定义法证明f（x）在R上是增函数；
（2）求出所有满足不等式f（2a-a2）+f（3）＞0的实数a构成的集合；
（3）对任意的实数x1∈[-1，1]，都存在一个实数x2∈[-1，1]，使得f（x1）=g（x2），求实数m的取值范围．
16．已知z=（2-i）3，则z的虚部=11．
3．已知z1，z2是复数，下列结论错误的是（　　）
A．若|z1-z2|=0，则$\overline{{z}_{1}}$=$\overline{{z}_{2}}$B．若 z1=$\overline{{z}_{2}}$，则$\overline{{z}_{1}}$=z2
C．若|z1|=|z2|，则z1•$\overline{{z}_{1}}$=z2$\overline{{z}_{2}}$D．若|z1|=|z2|，则z12=z22
13．已知实数a＞0，函数f（x）=ax3-4ax2+4ax（x∈R）
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）若函数f（x）有极大值16，求实数a的值．
20．已知非零向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为60°，$\overrightarrow{c}$=$\overrightarrow{a}$-k$\overrightarrow{b}$（k∈R），则$\frac{|\overrightarrow{a}|}{|\overrightarrow{c}|}$的最大值为$\frac{2\sqrt{3}}{3}$．
17．设x是纯虚数，y是实数，且2x-1+i=y-（3-y）i，则|x+y|=$\frac{7}{2}$．
18．“x＞1”是“x≠1”的充分不必要条件．（请在“充要”、“充分不必要”、“必要不充分”、“既不充分也不必要”中选择一个合适的填空）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网