题目内容
2.当x∈[-1,1]时,函数f(x)=ex(sinx-cosx)的最小值是-1.分析 求出函数f(x)的导数,求得f(x)在(-1,1)内的单调区间,即可得到极小值,也为最小值.
解答 解:函数f(x)=ex(sinx-cosx)的导数为
f′(x)=ex(sinx-cosx)+ex(cosx+sinx)
=2exsinx(x∈[-1,1]),
由f′(x)>0,可得0<x<1,即f(x)在(0,1)递增,
由f′(x)<0,可得-1<x<0,即f(x)在(-1,0)递减.
即有x=0处f(x)取得极小值,也为最小值,且为-1.
故答案为:-1.
点评 本题考查导数的运用:求单调区间和极值、最值,正确求导是解题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
18.5位男生与5位女生排成一排,男生甲与男生乙之间有且只有2位女生,女生不排在两端,这样的排列种数为( )
| A. | 5760 | B. | 57600 | C. | 2880 | D. | 28800 |
7.已知集合A={x|x2=2},B={1,$\sqrt{2}$,2},则A∩B=( )
| A. | {$\sqrt{2}$} | B. | {2} | C. | {-$\sqrt{2}$,1,$\sqrt{2}$,2} | D. | {-2,1,$\sqrt{2}$,2} |
11. 如图,一隧道截面由一个长方形和抛物线构成,现欲在隧道抛物线拱顶上安装交通信息采集装置,若位置C对隧道底AB的张角θ最大时采集效果最好,则采集效果最好时位置C到AB的距离是( )
如图,一隧道截面由一个长方形和抛物线构成,现欲在隧道抛物线拱顶上安装交通信息采集装置,若位置C对隧道底AB的张角θ最大时采集效果最好,则采集效果最好时位置C到AB的距离是( )
 如图,一隧道截面由一个长方形和抛物线构成,现欲在隧道抛物线拱顶上安装交通信息采集装置,若位置C对隧道底AB的张角θ最大时采集效果最好,则采集效果最好时位置C到AB的距离是( )
如图,一隧道截面由一个长方形和抛物线构成,现欲在隧道抛物线拱顶上安装交通信息采集装置,若位置C对隧道底AB的张角θ最大时采集效果最好,则采集效果最好时位置C到AB的距离是( )| A. | 2$\sqrt{2}$m | B. | 2$\sqrt{3}$m | C. | 4m | D. | 6m |
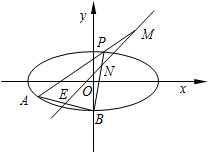 如图,已知椭圆$C:\frac{x^2}{12}+\frac{y^2}{4}=1$,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在x轴下方),且线段AB的中点E在直线y=x上.
如图,已知椭圆$C:\frac{x^2}{12}+\frac{y^2}{4}=1$,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在x轴下方),且线段AB的中点E在直线y=x上.