题目内容

7．已知集合A={x|x2=2}，B={1，$\sqrt{2}$，2}，则A∩B=（　　）
A．{$\sqrt{2}$}B．{2}C．{-$\sqrt{2}$，1，$\sqrt{2}$，2}D．{-2，1，$\sqrt{2}$，2}

分析 根据集合的基本运算进行求解即可．

解答 解：A={x|x2=2}={-$\sqrt{2}$，$\sqrt{2}$}，B={1，$\sqrt{2}$，2}，
则A∩B={$\sqrt{2}$}，
故选：A．

点评 本题主要考查集合的基本运算，比较基础．

练习册系列答案
相关题目
3．已知函数f（x）=ex+sinx-ax
（Ⅰ）求使得x=0成为f（x）极值点的a的值；
（Ⅱ）当a∈（0，2]，x∈[0，+∞）时，求f（x）最小值．
18．已知圆M：（x+$\sqrt{3}$）2+y2=24，定点N（$\sqrt{3}$，0），点P为圆M上的动点，点Q在NP上；点G在MP上，且满足$\overrightarrow{NP}$=-2$\overrightarrow{PQ}$，$\overrightarrow{CQ}$•$\overrightarrow{NP}$=0
（1）求点G的轨迹C的方程
（2）过点（2，0）作直线l与轴线C交于A，B两点；O是坐标原点，设$\overrightarrow{OS}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$；是否存在这样的直线l，使四边形OASB的对角线相等（即|OS|=|AB|）？若存在，求出直线l的方程；若不存在，请说明理由．
15．在同一坐标系中，将椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1变换成单位圆的伸缩变换是（　　）
A．φ：$\left\{\begin{array}{l}{x′=5x}\\{{y}^{′}=4y}\end{array}\right.$B．φ：$\left\{\begin{array}{l}{{x}^{′}=4x}\\{{y}^{′}=5y}\end{array}\right.$
C．φ：$\left\{\begin{array}{l}{{x}^{′}=\frac{1}{4}x}\\{{y}^{′}=\frac{1}{5}y}\end{array}\right.$D．φ：$\left\{\begin{array}{l}{{x}^{′}=\frac{1}{5}x}\\{{y}^{′}=\frac{1}{4}y}\end{array}\right.$
2．当x∈[-1，1]时，函数f（x）=ex（sinx-cosx）的最小值是-1．
12．设函数f（x）=ln（1+x），g（x）=xf′（x），其中f′（x）是f（x）的导函数．
（1）求f（x）在x=0处的切线方程；
（2）若f（x）≥ag（x）（x≥0）恒成立，求实数a的取值范围；
（3）设n∈N+，比较g（1）+g（2）+…+g（n）与n-f（n）的大小，并加以证明．
19．曲线y=2x-x3在点（1，1）处的切线方程为x+y-2=0．
16．下列四个命题中，真命题的个数是②③
①若b2=ac，则a、b、c成等比数列；
②若{an}为等差数列，且常数c＞0，则数列{c${\;}^{{a}_{n}}$}为等比数列．
③若{an}为等比数列，则数列{|an|}为等比数列；
④常数列既是等比数列，又是等差数列．
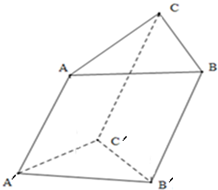17．斜三棱柱底面边长是4cm的正三角形，．侧棱长3cm，侧棱∠AA′C′=∠AA′B′=60°．
（1）求证：C′B′⊥AA′；
（2）求三棱柱的侧面积；
（3）求三棱柱的体积．
（提示：过点A作底面A′B′C′的垂线，垂足为P．则点P在∠C′A′B′的角平分线上）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网