题目内容
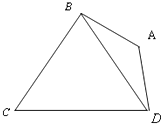
如图,在平面四边形ABCD中,△BCD是正三角形,AB=AD=1,∠BAD=θ.
(Ⅰ)将四边形ABCD的面积S表示成关于θ的函数;
(Ⅱ)求S的最大值及此时θ的值.
(Ⅰ)将四边形ABCD的面积S表示成关于θ的函数;
(Ⅱ)求S的最大值及此时θ的值.

(Ⅰ)BD=
=
,
S△ABD=
×1×1×sinθ=
sinθ,
S△BCD=
×BD2=
(2-2cosθ)=
-
cosθ,
∴SABCD=
sinθ-
cosθ+
(0<θ<π).
(Ⅱ)由(Ⅰ)得SABCD=
sinθ-
cosθ+
=sin(θ-
)+
,
∵0<θ<π,∴-
<θ-
<
,
当θ-
=
时,即θ=
时,S有最大值1+
.
| 12+12-2×1×1cosθ |
| 2-2cosθ |
S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
S△BCD=
| ||
| 4 |
| ||
| 4 |
| ||
| 2 |
| ||
| 2 |
∴SABCD=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
(Ⅱ)由(Ⅰ)得SABCD=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| π |
| 3 |
| ||
| 2 |
∵0<θ<π,∴-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
当θ-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
| ||
| 2 |

练习册系列答案
相关题目
 函数
函数 满足
满足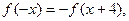 且当
且当 时,
时, 且
且 ,则
,则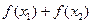 的值( )
的值( )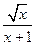 的最大值为 ( )
的最大值为 ( )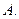
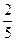
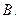
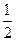
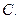
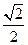
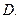 1
1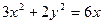 ,试求
,试求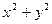 的最大值.
的最大值.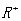 上的函数
上的函数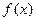 满足下列条件:1对定义域内任意
满足下列条件:1对定义域内任意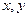 ,恒有
,恒有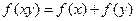 ;2当
;2当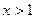 时
时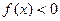 ;3
;3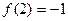 (1)求
(1)求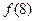 的值;
的值;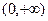 上为减函数;(3)解不等式 :
上为减函数;(3)解不等式 :