题目内容
18.曲线y=x3-2x+4在点(1,3)处的切线方程为( )| A. | y=x+2 | B. | y=-x+1 | C. | y=x-2 | D. | y=-x+4 |
分析 由求导公式和法则求出y′,把x=1代入求出切线的斜率,利用点斜式方程求出切线方程即可
解答 解:由题意得,y′=3x2-2,
所以在点(1,3)处的切线斜率k=3-2=1,
则在点(1,3)处的切线方程是y-3=x-1,即y=x+2,
故选:A.
点评 本题考查了导数的运算及法则,导数的几何意义,以及直线的点斜式方程的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.在对人们的休闲方式的一次调查中,共调查了120人,其中女性65人,男性55人.女性中有40人主要的休闲方式是看电视,另外25人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外35人主要的休闲方式是运动.${K^2}=\frac{{n{{({ab-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
其中n=a+b+c+d
(1)根据以上数据建立一个2×2的列联表;
(2)能够以多大的把握认为性别与休闲方式有关系,为什么?
其中n=a+b+c+d
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)能够以多大的把握认为性别与休闲方式有关系,为什么?
9.在△ABC中,AB=3,AC=2,$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$,则直线AD通过△ABC的( )
| A. | 垂心 | B. | 外心 | C. | 内心 | D. | 重心 |
3.已知函数f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+$\frac{1}{6}$的图象与x轴有且只有一个交点,则a的取值范围是( )
| A. | (-∞,1) | B. | [0,1) | C. | (-∞,0] | D. | (1,+∞) |
10.抛物线的顶点在原点,准线方程为x=3,则抛物线方程为( )
| A. | y2=-12x | B. | y2=-6x | C. | y2=12x | D. | y2=6x |
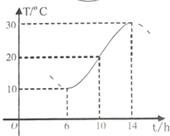 如图,某地一天从6-14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则该函数的表达式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
如图,某地一天从6-14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则该函数的表达式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].