题目内容
15.函数f(x)=x3的图象在点(1,f(1))处切线的斜率是3.分析 由求导公式求出f′(x),再由导数的几何意义求出切线的斜率k=f′(1)的值.
解答 解:由题意得,f′(x)=3x2,
所以在点(1,f(1))处切线的斜率k=f′(1)=3,
故答案为:3.
点评 本题考查求导公式,以及导数的几何意义的应用,属于基础题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
5.已知集合A={x|2<x<5},B={x|(x-1)(x-3)<0},则A∩B=( )
| A. | (1,3) | B. | (1,5) | C. | (2,3) | D. | (2,5) |
3.已知函数f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+$\frac{1}{6}$的图象与x轴有且只有一个交点,则a的取值范围是( )
| A. | (-∞,1) | B. | [0,1) | C. | (-∞,0] | D. | (1,+∞) |
10.抛物线的顶点在原点,准线方程为x=3,则抛物线方程为( )
| A. | y2=-12x | B. | y2=-6x | C. | y2=12x | D. | y2=6x |
20.已知定义在(0,$\frac{π}{2}$)上的函数f(x),f′(x)为其导函数,且f(x)<f′(x)•tanx恒成立,则( )
| A. | $\sqrt{3}f(\frac{π}{6})$<$f(\frac{π}{3})$ | B. | $\sqrt{3}f(\frac{π}{4})$>$\sqrt{2}f(\frac{π}{3})$ | C. | $\sqrt{2}f(\frac{π}{6})$>$f(\frac{π}{4})$ | D. | f(1)$<2f(\frac{π}{6})•sin1$ |
20.已知在△ABC中,a=$\sqrt{5},b=\sqrt{15},A={30°}$,则c等于( )
| A. | 2$\sqrt{5}$ | B. | $\sqrt{5}$或2$\sqrt{5}$ | C. | $\sqrt{15}$ | D. | 以上都不对 |
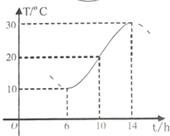 如图,某地一天从6-14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则该函数的表达式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
如图,某地一天从6-14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则该函数的表达式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].