题目内容
11.甲、乙两人独立地解决同一个问题,甲能解决这个问题的概率是P1,乙能解决这个问题的概率是P2,那么至少有一人能解决这个问题的概率是( )| A. | P1+P2 | B. | P1P2 | C. | 1-P1P2 | D. | 1-(1-P1)(1-P2) |
分析 根据对立事件的概率公式先求出都不能解决问题的概率即可得到结论.
解答 解:甲能解决这个问题的概率是P1,乙能解决这个问题的概率是P2,
则甲不能解决这个问题的概率是1-P1,乙不能解决这个问题的概率是1-P2,
则甲易都不能解决这个问题的概率是(1-P1)(1-P2),
则至少有一人能解决这个问题的概率是1-(1-P1)(1-P2),
故选:D
点评 本题主要考查独立事件同时发生的概率的计算,根据对立事件的概率关系先求出都不能解决问题的概率是解决本题的关键.

练习册系列答案
相关题目
19.设集合M={x|-2≤x≤2},N={x|x≥2},则M∩N等于( )
| A. | [-2,2] | B. | {2} | C. | [2,+∞) | D. | [-2,+∞) |
16.已知二次函数f(x)=x2-2x+ab(a≠b)有唯一的零点,则代数式|$\frac{{a}^{2}+{b}^{2}+2}{a-b}$|的最小值是( )
| A. | 8$\sqrt{2}$ | B. | 6 | C. | 4$\sqrt{2}$ | D. | 4 |
3.已知函数f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+$\frac{1}{6}$的图象与x轴有且只有一个交点,则a的取值范围是( )
| A. | (-∞,1) | B. | [0,1) | C. | (-∞,0] | D. | (1,+∞) |
20.已知定义在(0,$\frac{π}{2}$)上的函数f(x),f′(x)为其导函数,且f(x)<f′(x)•tanx恒成立,则( )
| A. | $\sqrt{3}f(\frac{π}{6})$<$f(\frac{π}{3})$ | B. | $\sqrt{3}f(\frac{π}{4})$>$\sqrt{2}f(\frac{π}{3})$ | C. | $\sqrt{2}f(\frac{π}{6})$>$f(\frac{π}{4})$ | D. | f(1)$<2f(\frac{π}{6})•sin1$ |
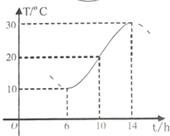 如图,某地一天从6-14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则该函数的表达式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
如图,某地一天从6-14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则该函数的表达式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].