题目内容
16.已知D为△ABC的边BC上的中点,△ABC所在平面内有一点P,满足$\overrightarrow{PA}$+$\overrightarrow{BP}$+$\overrightarrow{CP}$=0,则$\frac{|\overrightarrow{PD}|}{|\overrightarrow{AD}|}$等于( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
分析 由于D为△ABC的边BC的中点,可得$\overrightarrow{PB}+\overrightarrow{PC}$=2$\overrightarrow{PD}$.由于满足$\overrightarrow{PA}$+$\overrightarrow{BP}$+$\overrightarrow{CP}$=$\overrightarrow{0}$,可得$\overrightarrow{PA}$=2$\overrightarrow{PD}$.即可得出答案.
解答 解:由于D为BC边上的中点,
因此由向量加法的平行四边形法则,易知$\overrightarrow{PB}+\overrightarrow{PC}$=2$\overrightarrow{PD}$,
即2$\overrightarrow{PD}$-($\overrightarrow{PB}+\overrightarrow{PC}$)=2$\overrightarrow{PD}$+$\overrightarrow{BP}$+$\overrightarrow{CP}$=$\overrightarrow{0}$
因此结合$\overrightarrow{PA}$+$\overrightarrow{BP}$+$\overrightarrow{CP}$=$\overrightarrow{0}$即得:$\overrightarrow{PA}$=2$\overrightarrow{PD}$.
因此易得P,A,D三点共线且D是PA的中点,
所以$\frac{|\overrightarrow{PD}|}{|\overrightarrow{AD}|}$=1.
故选:C
点评 本题考查了向量的平行四边形法则、向量的共线与线性运算,属于基础题.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案其中n=a+b+c+d
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)能够以多大的把握认为性别与休闲方式有关系,为什么?
| A. | (1,3) | B. | (1,5) | C. | (2,3) | D. | (2,5) |
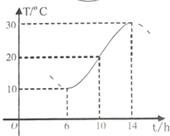 如图,某地一天从6-14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则该函数的表达式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
如图,某地一天从6-14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则该函数的表达式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].