题目内容
14.若直线y=k(x+1)与圆x2+y2=1相交于A,B两点,且$\overrightarrow{OA}$$•\overrightarrow{OB}$=-$\frac{1}{2}$,则实数k的值为( )| A. | $±\frac{\sqrt{3}}{3}$ | B. | $±\frac{\sqrt{3}}{2}$ | C. | ±1 | D. | $±\sqrt{3}$ |
分析 先求出弦心距d,再由题意可得cos60°=$\frac{1}{2}$=$\frac{|k|}{\sqrt{{k}^{2}+1}}$,求得k的值.
解答 解:弦心距d=$\frac{|k|}{\sqrt{{k}^{2}+1}}$
由题意,$\overrightarrow{OA}$$•\overrightarrow{OB}$=-$\frac{1}{2}$,可得∠AOB=120°,
∴cos60°=$\frac{1}{2}$=$\frac{|k|}{\sqrt{{k}^{2}+1}}$,
解得k=±$\frac{\sqrt{3}}{3}$,
故选:A.
点评 本题主要考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,属于基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
5.已知集合A={x|2<x<5},B={x|(x-1)(x-3)<0},则A∩B=( )
| A. | (1,3) | B. | (1,5) | C. | (2,3) | D. | (2,5) |
9.在△ABC中,AB=3,AC=2,$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$,则直线AD通过△ABC的( )
| A. | 垂心 | B. | 外心 | C. | 内心 | D. | 重心 |
19.设集合M={x|-2≤x≤2},N={x|x≥2},则M∩N等于( )
| A. | [-2,2] | B. | {2} | C. | [2,+∞) | D. | [-2,+∞) |
3.已知函数f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+$\frac{1}{6}$的图象与x轴有且只有一个交点,则a的取值范围是( )
| A. | (-∞,1) | B. | [0,1) | C. | (-∞,0] | D. | (1,+∞) |
20.已知在△ABC中,a=$\sqrt{5},b=\sqrt{15},A={30°}$,则c等于( )
| A. | 2$\sqrt{5}$ | B. | $\sqrt{5}$或2$\sqrt{5}$ | C. | $\sqrt{15}$ | D. | 以上都不对 |
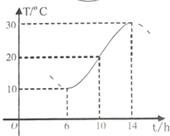 如图,某地一天从6-14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则该函数的表达式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
如图,某地一天从6-14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则该函数的表达式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].