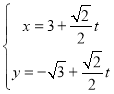题目内容
【题目】已知F1,F2是椭圆C:![]() (a>b>0)的左、右焦点,过椭圆的上顶点的直线x+y=1被椭圆截得的弦的中点坐标为
(a>b>0)的左、右焦点,过椭圆的上顶点的直线x+y=1被椭圆截得的弦的中点坐标为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过F1的直线l交椭圆于A,B两点,当△ABF2面积最大时,求直线l的方程.
【答案】(Ⅰ)![]() y2=1;(Ⅱ)x﹣y
y2=1;(Ⅱ)x﹣y![]() 0或x+y
0或x+y![]() 0.
0.
【解析】
(Ⅰ)根据直线椭圆的过上顶点,得b=1,再利用点差法以及弦中点坐标解得a2=3,即得椭圆方程;
(Ⅱ)先设直线l方程并与椭圆方程联立,结合韦达定理,并以|F1F2|为底边长求△ABF2面积函数关系式,在根据基本不等式求△ABF2面积最大值,进而确定直线l的方程.
(Ⅰ)直线x+y=1与y轴的交于(0,1)点,∴b=1,
设直线x+y=1与椭圆C交于点M(x1,y1),N(x2,y2),
则x1+x2![]() ,y1+y2
,y1+y2![]() ,
,
∴![]() 1,
1,![]() 1,
1,
两式相减可得![]() (x1﹣x2)(x1+x2)
(x1﹣x2)(x1+x2)![]() (y1﹣y2)(y1+y2)=0,
(y1﹣y2)(y1+y2)=0,
∴![]() ,
,
∴![]()
![]()
![]() 1,
1,
解得a2=3,
∴椭圆C的方程为![]() y2=1.
y2=1.
(Ⅱ)由(Ⅰ)可得F1(![]() ,0),F2(
,0),F2(![]() ,0),设A(x3,y3),B(x4,y4),
,0),设A(x3,y3),B(x4,y4),
可设直线l的方程x=my![]() ,将直线l的方程x=my
,将直线l的方程x=my![]() 代入
代入![]() y2=1,可得(m2+3)y2﹣2
y2=1,可得(m2+3)y2﹣2![]() my﹣1=0,
my﹣1=0,
则y3+y4![]() ,y3y4
,y3y4![]() ,
,
|y3﹣y4|![]() ,
,
∴![]() |F1F2|
|F1F2|![]() |y3﹣y4|
|y3﹣y4|![]() |
|![]() |y3﹣y4|
|y3﹣y4| ,
,
当且仅当![]() ,即m=±1,△ABF2面积最大,
,即m=±1,△ABF2面积最大,
即直线l的方程为x﹣y![]() 0或x+y
0或x+y![]() 0.
0.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案【题目】某药业公司统计了2010-2019年这10年某种疾病的患者人数,结论如下:该疾病全国每年的患者人数都不低于100万,其中有3年的患者人数低于200万,有6年的患者人数不低于200万且低于300万,有1年的患者人数不低于300万.
(1)药业公司为了解一新药品对该疾病的疗效,选择了200名患者,随机平均分为两组作为实验组和对照组,实验结束时,有显著疗效的共110人,实验组中有显著疗效的比率为70%.请完成如下的2×2列联表,并根据列联表判断是否有99.9%把握认为该药品对该疾病有显著疗效;
实验组 | 对照组 | 合计 | |
有显著疗效 | |||
无显著疗效 | |||
合计 | 200 |
(2)药业公司最多能引进3条新药品的生产线,据测算,公司按如下条件运行生产线:
该疾病患者人数(单位:万) |
|
|
|
最多可运行生产线数 | 1 | 2 | 3 |
每运行一条生产线,可产生年利润6000万元,没运行的生产线毎条每年要亏损1000万元.根据该药业公司这10年的统计数据,将患者人数在以上三段的频率视为相应段的概率、假设各年的患者人数相互独立.欲使该药业公司年总利润的期望值达到最大,应引进多少条生产线?
附:参考公式: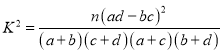 ,其中
,其中![]() .
.
| 0.05 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |