题目内容
设 、
、 分别是定义在
分别是定义在 上的奇函数和偶函数,当
上的奇函数和偶函数,当 时,
时, ,且
,且 ,则不等式
,则不等式 的解集是( )
的解集是( )
A. | B. |
C. | D. |
D
解析试题分析: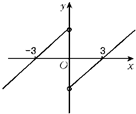
解:设F(x)="f" (x)g(x),当x<0时,∵F′(x)=f′(x)g(x)+f (x)g′(x)>0.∴F(x)在当x<0时为增函数.∵F(-x)="f" (-x)g (-x)="-f" (x)•g (x)=-F(x).故F(x)为(-∞,0)∪(0,+∞)上的奇函数.∴F(x)在(0,∞)上亦为增函数.已知g(-3)=0,必有F(-3)=F(3)=0.构造如图的F(x)的图象,可知,F(x)<0的解集为x∈(-∞,-3)∪(0,3)故选D
考点:复合函数的求导运算
点评:本题主要考查复合函数的求导运算和函数的单调性与其导函数正负之间的关系.导数是一个新内容,也是高考的热点问题,要多注意复习

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
下列函数中,在区间 上为增函数的是( ).
上为增函数的是( ).
A.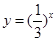 | B.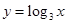 | C.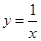 | D.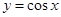 |
若函数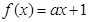 在R上递减,则函数
在R上递减,则函数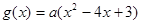 的增区间是 ( )
的增区间是 ( )
| A.(2,+∞) | B.(-∞,2) | C.(-2,+∞) | D.(-∞,-2) |
函数满足f(x)f(x+2)=13,若f(3)=2,则f(2013)= ( )
| A.13 | B.2 | C. | D. |
下列函数中,在其定义域内既是奇函数又是增函数的是
A.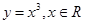 | B.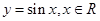 | C.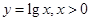 | D.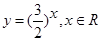 |
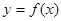 的图象如右下图所示, 则函数
的图象如右下图所示, 则函数 的图象大致为( )
的图象大致为( )

 -2sin x的图象大致是( )
-2sin x的图象大致是( )
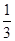

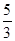
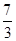
 上的函数
上的函数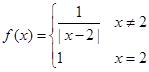 ,若关于
,若关于 的方程
的方程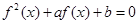 有3个不同实数解
有3个不同实数解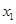 、
、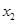 、
、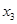 ,且
,且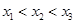 ,则下列说法中错误的是( )
,则下列说法中错误的是( )